题目内容
【题目】已知等比数列![]() 满足:
满足:![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
【答案】(1)an=![]() ·3n-1,或an=-5·(-1)n-1.
·3n-1,或an=-5·(-1)n-1.
(2)不存在正整数m,使得![]() ≥1成立.
≥1成立.
【解析】
试题(1)将已知条件转化为等比数列的首项和公比表示,转化为关于![]() 的方程组,通过解方程组得到
的方程组,通过解方程组得到![]() 的值,从而得到数列的通项公式;(2)将数列
的值,从而得到数列的通项公式;(2)将数列![]() 的通项公式代入
的通项公式代入![]() 求和,分情况判断对应的不等式是否成立
求和,分情况判断对应的不等式是否成立
试题解析:(1)设等比数列{an}的公比为q,
则由已知可得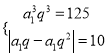
解得![]() 或
或![]()
故an=![]() ·3n-1,或an=-5·(-1)n-1.
·3n-1,或an=-5·(-1)n-1.
(2)若an=![]() ·3n-1,则
·3n-1,则![]() =
=![]() ·(
·(![]() )n-1.
)n-1.
故{![]() }是首项为
}是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
从而 .
.
若an=-5·(-1)n-1,则![]() =-
=-![]() (-1)n-1.
(-1)n-1.
故{![]() }是首项为-
}是首项为-![]() ,公比为-1的等比数列.
,公比为-1的等比数列.
从而![]() =
=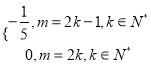 故
故![]() <1.
<1.
综上,对任何正整数m,总有![]() <1.
<1.
故不存在正整数m,使得![]() ≥1成立.
≥1成立.

练习册系列答案
相关题目