Question

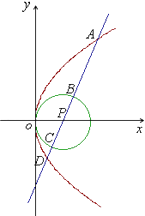
【题目】给定圆P：x2+y2=2x及抛物线S：y2=4x，过圆心P作直线l，此直线与上述两曲线的四个交点，自上而下顺次为A，B，C，D；如果线段AB，BC，CD的长度按此顺序构成一个等差数列，则直线l的方程为

Answer 1

【答案】
【解析】解：圆P的方程为（x﹣1）2+y2=1，则其直径长|BC|=2，圆心为P（1，0），
设l的方程为ky=x﹣1，即x=ky+1，代入抛物线方程得：y2=4ky+4，
设A（x1 ， y1），D（x2 ， y2），
有y1+y2=4k，y1y2=﹣4，
则（y1﹣y2）2=（y1+y2）2+4y1y2=16（k2+1）
故|AD|2=（y1﹣y2）2+（x1﹣x2）2=16（k2+1）2 ，
因此|AD|=4（k2+1）．
因为线段AB、BC、CD的长按此顺序构成一个等差数列，
所以|AD|=3|BC|，即4（k2+1）=6
∴k=±
∴l方程 ．
所以答案是： ．