题目内容
【题目】已知函数![]() ,直线
,直线![]() 为曲线
为曲线![]() 的切线(
的切线(![]() 为自然对数的底数).
为自然对数的底数).
(1)求实数![]() 的值;
的值;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,若函数
,若函数
![]() 为增函数,求实数
为增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)先求导,然后利用导数等于![]() 求出切点的横坐标,代入两个曲线的方程,解方程组,可求得
求出切点的横坐标,代入两个曲线的方程,解方程组,可求得![]() ;(2)设
;(2)设![]() 与
与![]() 交点的横坐标为
交点的横坐标为![]() ,利用导数求得
,利用导数求得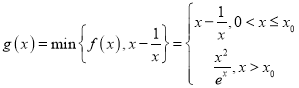 ,从而
,从而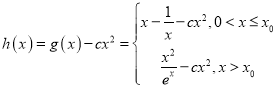 ,然后利用
,然后利用![]() 求得
求得![]() 的取值范围为
的取值范围为![]() .
.
试题解析:
(1)对![]() 求导得
求导得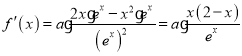 .....................1分
.....................1分
设直线![]() 与曲线
与曲线![]() 切于点
切于点![]() ,则
,则
 ,解得
,解得![]() ,
,
所以![]() 的值为1..........................................3分
的值为1..........................................3分
(2)记函数![]() ,下面考察函数
,下面考察函数![]() 的符号,
的符号,
对函数![]() 求导得
求导得![]() ......................4分
......................4分
当![]() 时,
时,![]() 恒成立.................................5分
恒成立.................................5分
当![]() 时,
时,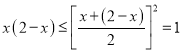 ,
,
从而![]() .....................7分
.....................7分
∴![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 在
在![]() 上单调递减.
上单调递减.
![]() ,∴
,∴![]() ,
,
又曲线 ![]() 在
在![]() 上连续不间断,所以由函数的零点存在性定理及其单调性知
上连续不间断,所以由函数的零点存在性定理及其单调性知![]() 唯一的
唯一的![]() ,使
,使![]() .
.
∴![]() ;
;![]() ,
,![]() ,
,
∴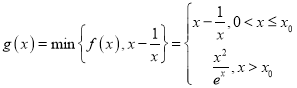 ,
,
从而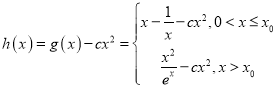 ,
,
∴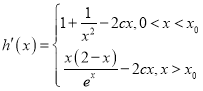 ,..........................9分
,..........................9分
由函数![]() 为增函数,且曲线
为增函数,且曲线![]() 在
在![]() 上连续不断知
上连续不断知![]() 在
在![]() ,
,![]() 上恒成立.
上恒成立.
①当![]() 时,
时,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
记![]() ,则
,则![]() ,
,
当![]() 变化时,
变化时,![]() 变化情况列表如下:
变化情况列表如下:
|
| 3 |
|
|
| 0 |
|
|
| 极小值 |
|
∴![]() ,
,
故“![]() 在
在![]() 上恒成立”只需
上恒成立”只需![]() ,即
,即 ![]() .
.
②当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
综合①②知,当![]() 时,函数
时,函数![]() 为增函数.
为增函数.
故实数![]() 的取值范围是
的取值范围是![]() ...............................12分
...............................12分

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目

