题目内容
【题目】若函数![]() 在
在![]() 上是单调函数,则a的取值范围是( )
上是单调函数,则a的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
由求导公式和法则求出f′(x),由条件和导数与函数单调性的关系分类讨论,分别列出不等式进行分离常数,再构造函数后,利用整体思想和二次函数的性质求出函数的最值,可得a的取值范围.
解:由题意得,f′(x)![]() ,
,
因为![]() 在[1,+∞)上是单调函数,
在[1,+∞)上是单调函数,
所以f′(x)≥0或f′(x)≤0在[1,+∞)上恒成立,
①当f′(x)≥0时,则![]() 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a![]() ,设g(x)
,设g(x)![]() ,
,
因为x∈[1,+∞),所以![]() ∈(0,1],
∈(0,1],
当![]() 1时,g(x)取到最大值是:0,
1时,g(x)取到最大值是:0,
所以a≥0,
②当f′(x)≤0时,则![]() 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a![]() ,设g(x)
,设g(x)![]() ,
,
因为x∈[1,+∞),所以![]() ∈(0,1],
∈(0,1],
当![]() 时,g(x)取到最大值是:
时,g(x)取到最大值是:![]() ,
,
所以a![]() ,
,
综上可得,a![]() 或a≥0,
或a≥0,
所以数a的取值范围是(﹣∞,![]() ]∪[0,+∞),
]∪[0,+∞),
故选:B.

【题目】某企业共有员工10000人,下图是通过随机抽样得到的该企业部分员工年收入(单位:万元)频率分布直方图.
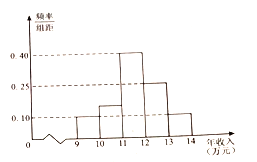
(1)根据频率分布直方图计算样本的平均数.并以此估算该企业全体员工中年收入不低于样本平均数的人数(同一组中的数据以这数据所在区间中点的值作代表);
(2)若抽样调查中收入在![]() 万元员工有2人,求在收入在
万元员工有2人,求在收入在![]() 万元的员工中任取3人,恰有2位员工收入在
万元的员工中任取3人,恰有2位员工收入在![]() 万元的概率;
万元的概率;
(3)若抽样调查的样本容量是400人,在这400人中:年收入在![]() 万元的员工中具有大学及大学以上学历的有
万元的员工中具有大学及大学以上学历的有![]() ,年收入在
,年收入在![]() 万元的员工中不具有大学及大学以上学历的有
万元的员工中不具有大学及大学以上学历的有![]() ,将具有大学及大学以上学历和不具有大学及大学以上学历的员工人数填入下面的列联表,并判断能否有
,将具有大学及大学以上学历和不具有大学及大学以上学历的员工人数填入下面的列联表,并判断能否有![]() 的把握认为具有大学及大学以上学历和不具有大学及大学以上学历的员工收入有差异?
的把握认为具有大学及大学以上学历和不具有大学及大学以上学历的员工收入有差异?
具有大学及大学以上学历 | 不具有大学及大学以上学历 | 合计 | |
| |||
| |||
合计 |
附:![]() ;
;
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |