Question

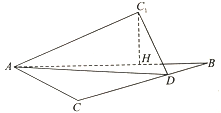
【题目】已知梯形ABCD中，，如图（1）所示.现将△ABC沿边BC翻折至A'BC，记二面角A'—BC—D的大小为θ.

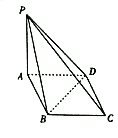
（1）当θ＝90°时，如图（2）所示，过点B作平面与A‘D垂直，分别交于点E，F，求点E到平面的距离；

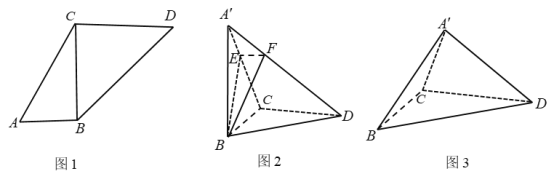
（2）当时，如图（3）所示，求二面角的正切值

Answer 1

【答案】（1）；（2）.

【解析】

（1）求得的长，利用等体积法计算出点E到平面的距离.

（2）作出二面角的平面角，由此求得其正切值.

（1）因为平面平面，平面平面，

，平面，

所以平面，又平面，所以，

因为平面，平面，所以

又，平面，

所以平面，又平面，所以，

在中，，

又平面平面，平面平面，

，平面，

所以平面，又平面，所以，

在中，，

所以，

在中，，

设点到平面的距离为，

因为，所以，

，所以；

（2）过点作直线//，过作交于点.

因为，所以，又因为，

所以就是二面角的平面角，

所以，因为，所以，

过点作交于点，连接，

因为，，，所以平面，

又平面，所以平面平面.

又因为平面平面，，平面

所以平面，

因为，，所以平面，

因为平面，所以，

所以是二面角的平面角，

在中，，

，

所以二面角的正切值为.