题目内容

6．在△ABC中，角A、B、C所对的边分别为a、b、c，且满足c2=a2+b2+ab，则角C的大小为（　　）
A．120°B．60°C．150°D．30°

分析 利用余弦定理表示出cosC，把已知的等式变形后代入求出cosC的值，由C的范围，利用特殊角的三角函数值即可求出角C的度数．

解答 解：由a2+b2+ab=c2，得到a2+b2-c2=-ab，
则根据余弦定理得：
cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$，又C∈（0，180°），
则角C的大小为120°．
故选：A．

点评 此题考查了余弦定理的应用，要求学生熟练掌握余弦定理的特征，牢记特殊角的三角函数值．学生做题时注意角度的范围，属于基础题．

练习册系列答案
相关题目
3．已知极坐标系的极点在直角坐标系的原点，极轴与x轴的正半轴重合，直线l的参数方程为$\left\{\begin{array}{l}x=-\frac{{\sqrt{2}}}{2}t+\sqrt{2}\\ y=\frac{{\sqrt{2}}}{2}t\end{array}$（t为参数），圆C的极坐标方程为ρ2+$2ρsin（θ+\frac{π}{4}）$+1=r2（r＞0）．
（1）求直线l的普通方程和圆C的直角坐标方程；
（2）若圆C上的点到直线l的最大距离为3，求r的值．
17．向量$\overrightarrow{OA}$=（x，y）（O为原点）的终点A位于第二象限，则有（　　）
A．x＞0，y＞0B．x＞0，y＜0C．x＜0，y＞0D．x＜0，y＜0
14．函数$f（x）=\frac{1}{x-5}{log_2}（x-3）$的定义域是（　　）
A．（-∞，5）∪（5，+∞）B．（3，+∞）C．（3，5）D．（3，5）∪（5，+∞）
1．在△ABC中三边之比a：b：c=2：3：$\sqrt{19}$，则△ABC中最大角的大小为（　　）
A．$\frac{π}{2}$B．$\frac{2π}{3}$C．$\frac{3π}{4}$D．$\frac{5π}{6}$
11．设数列{an}，{bn}满足an+1-an=bn，bn+1=2bn（其中n∈N*），a1≠b1，且b1≠0，若$[\begin{array}{l}{{a}_{n+4}}\\{{b}_{n+4}}\end{array}]$=M$[\begin{array}{l}{{a}_{n}}\\{{b}_{n}}\end{array}]$，则二阶矩阵M-1=$[\begin{array}{l}{1}&{-\frac{15}{16}}\\{0}&{\frac{1}{16}}\end{array}]$．
18．设函数$f（x）=\left\{\begin{array}{l}x-[x]，x≤0\\ f（x-1），x＞0\end{array}\right.$，其中[x]表示不超过x的最大整数．若方程f（x）=ax有三个不同的实数根，则实数a的取值范围是（-1，-$\frac{1}{2}$]∪[$\frac{1}{4}$，$\frac{1}{3}$）．
15．在直角坐标系xoy中，“a＞b”是“方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1表示椭圆”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分条件又不必要条件
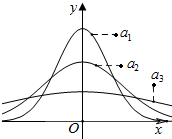16．如图分别是正态分布N（0，σ12），N（0，σ22），N（0，σ32）在同一坐标平面的分布密度曲线，则σ1、σ2、σ3的大小关系为σ1＜σ2＜σ3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网