题目内容
如图,在四棱锥P ABCD中,底面是边长为2
ABCD中,底面是边长为2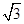 的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2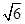 ,M、N分别为PB、PD的中点.
,M、N分别为PB、PD的中点.
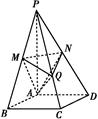
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角A MN
MN Q的平面角的余弦值.
Q的平面角的余弦值.
 ABCD中,底面是边长为2
ABCD中,底面是边长为2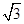 的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2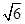 ,M、N分别为PB、PD的中点.
,M、N分别为PB、PD的中点.
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角A
 MN
MN Q的平面角的余弦值.
Q的平面角的余弦值.(1)见解析 (2)

(1)证明:连接BD,因为M、N分别是PB、PD的中点,所以MN是△PBD的中位线,所以MN∥BD.
又因为MN?平面ABCD,BD?平面ABCD,
所以MN∥平面ABCD.
(2)解: 如图所示,在菱形ABCD中,∠BAD=120°,

得AC=AB=BC=CD=DA,
BD=
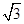 AB.
AB.又因为PA⊥平面ABCD,
所以PA⊥AB,PA⊥AC,
PA⊥AD.
所以PB=PC=PD.
所以△PBC≌△PDC.
而M、N分别是PB、PD的中点,
所以MQ=NQ,
且AM=
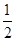 PB=
PB=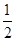 PD=AN.
PD=AN.取线段MN的中点E,连接AE,EQ,
则AE⊥MN,QE⊥MN,
所以∠AEQ为二面角A
 MN
MN Q的平面角.
Q的平面角.由AB=2
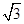 ,PA=2
,PA=2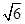 ,故在△AMN中,AM=AN=3,MN=
,故在△AMN中,AM=AN=3,MN=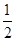 BD=3,得AE=
BD=3,得AE=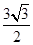 .
.在直角△PAC中,AQ⊥PC,得AQ=2
 ,QC=2,PQ=4,
,QC=2,PQ=4,在△PBC中,cos∠BPC=
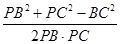 =
=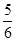 ,
,得MQ=
 =
=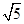 .
.在等腰△MQN中,MQ=NQ=
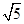 ,MN=3,
,MN=3,得QE=
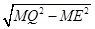 =
= .
.在△AEQ中,AE=
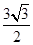 ,QE=
,QE= ,AQ=2
,AQ=2 ,
,得cos∠AEQ=
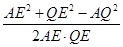 =
= .
.所以二面角A
 MN
MN Q的平面角的余弦值为
Q的平面角的余弦值为 .
.
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
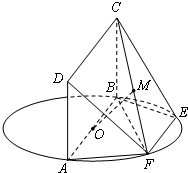
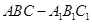 的所有顶点都在半径为
的所有顶点都在半径为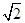 的球面上,
的球面上,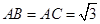 ,
,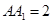 ,则二面角
,则二面角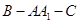 的余弦值为( )
的余弦值为( )



 ABCD中,底面正方形ABCD的边长为1,侧棱长为2,则异面直线VA与BD所成角的大小为( )
ABCD中,底面正方形ABCD的边长为1,侧棱长为2,则异面直线VA与BD所成角的大小为( )



 ,则BC1与平面BB1D1D所成角的正弦值为( ).
,则BC1与平面BB1D1D所成角的正弦值为( ).




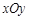 中,设
中,设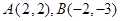 ,沿
,沿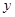 轴把坐标平面折成
轴把坐标平面折成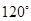 的二面角后,
的二面角后,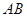 的长是 ( )
的长是 ( ) 
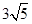

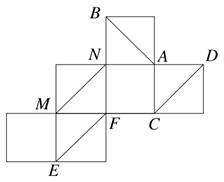
 ,E、F分别为AB、CD中点,且EF=4,则AD与BC所成的角是 .
,E、F分别为AB、CD中点,且EF=4,则AD与BC所成的角是 . 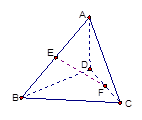
 的大小是60°,线段
的大小是60°,线段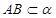 ,
, 在
在 上,
上,  与
与 所成的角为30°,则
所成的角为30°,则