题目内容
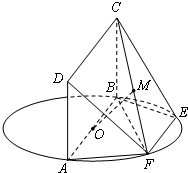
如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(1)求证:AF⊥平面CBF;
(2)设FC的中点为M,求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE.
(1)求证:AF⊥平面CBF;
(2)设FC的中点为M,求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE.

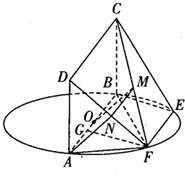
(1)证明:由平面ABCD⊥平面ABEF,CB⊥AB,
平面ABCD∩平面ABEF=AB,
得CB⊥平面ABEF,
而AF?平面ABEF,所以AF⊥CB(2分)
又因为AB为圆O的直径,
所以AF⊥BF,(3分)
又BF∩CB=B,所以AF⊥平面CBF(4分)
(2)证明:设DF的中点为N,连接AN,MN
则MN
CD,又AO
CD
则MN
AO,所以四边形MNAO为平行四边形,(6分)
所以OM∥AN,又AN?平面DAF,OM?平面DAF,
所以OM∥平面DAF.(8分)
(3)过点F作FG⊥AB于G,因为平面ABCD⊥平面ABEF,
所以FG⊥平面ABCD,所以VF-ABCD=
SABCD•FG=
FG(9分)
因为CB⊥平面ABEF,
所以VF-CBE=VC-BFE=
S△BFE•CB=
•
EF•FG•CB=
FG(11分)
所以VF-ABCD:VF-CBE=4:1.(12分)
平面ABCD∩平面ABEF=AB,
得CB⊥平面ABEF,
而AF?平面ABEF,所以AF⊥CB(2分)
又因为AB为圆O的直径,
所以AF⊥BF,(3分)
又BF∩CB=B,所以AF⊥平面CBF(4分)
(2)证明:设DF的中点为N,连接AN,MN
则MN
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
| 1 |
| 2 |
则MN
| ∥ |
| . |
所以OM∥AN,又AN?平面DAF,OM?平面DAF,
所以OM∥平面DAF.(8分)
(3)过点F作FG⊥AB于G,因为平面ABCD⊥平面ABEF,
所以FG⊥平面ABCD,所以VF-ABCD=
| 1 |
| 3 |
| 2 |
| 3 |
因为CB⊥平面ABEF,
所以VF-CBE=VC-BFE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
所以VF-ABCD:VF-CBE=4:1.(12分)


练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ABCD中,底面是边长为2
ABCD中,底面是边长为2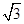 的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2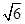 ,M、N分别为PB、PD的中点.
,M、N分别为PB、PD的中点.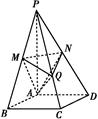

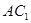 中,直线
中,直线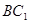 与平面
与平面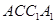 所成角的大小为____________.
所成角的大小为____________.