题目内容
(本小题9分)等差数列{an}不是常数列,a5=10,且a5,a7,a10是某一等比数列{bn}的第1,2,3项,(1)求数列{an}的第20项,(2)求数列{bn}的通项公式。
解:(1)设数列{an}的公差为d,则a5=10,a7=10+2d,a10=10+5d
因为等比数列{bn}的第1、2、3项也成等比,
所以a72=a5a10
即:(10+2d)2=10(10+5d)
解得d="2.5 " ,d=0(舍去)…………………………………………………4分
所以:a20=47.5………………………………………………………………5分
(2)由(1)知{an}为正项数列,所以q=b2/b1=a7/a5=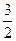 …………………7分
…………………7分
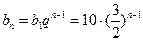 ……………………………… 9分
……………………………… 9分
因为等比数列{bn}的第1、2、3项也成等比,
所以a72=a5a10
即:(10+2d)2=10(10+5d)
解得d="2.5 " ,d=0(舍去)…………………………………………………4分
所以:a20=47.5………………………………………………………………5分
(2)由(1)知{an}为正项数列,所以q=b2/b1=a7/a5=
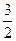 …………………7分
…………………7分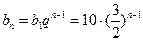 ……………………………… 9分
……………………………… 9分略

练习册系列答案
相关题目
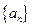 的前
的前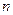 项的和
项的和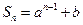 ,
,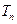 为数列
为数列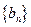 的前
的前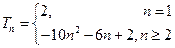 .
.
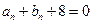 的自然数
的自然数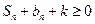 对于任意的
对于任意的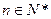 ,
,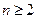 恒成立,求实数
恒成立,求实数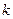 的最小值,并求出此时相应的
的最小值,并求出此时相应的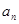 }的前n项和为
}的前n项和为 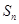 ,若
,若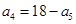 ,则
,则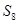 =( )
=( )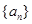 的前
的前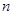 项和为
项和为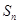 ,若
,若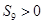 ,
,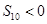 ,则
,则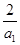 ,
,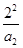 ,
, ,
,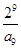 中最大的是( )
中最大的是( )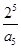
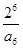
 }的通项公式;
}的通项公式;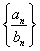 的前n项和
的前n项和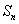 .
.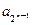 ,…,构成一个新的数列{bn},求{bn}的前n项和.
,…,构成一个新的数列{bn},求{bn}的前n项和.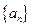 的前
的前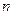 项和为
项和为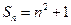 ,数列
,数列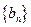 满足:
满足: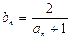 ,前
,前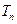 ,设
,设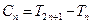 。 (1)求数列
。 (1)求数列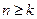 时,总有
时,总有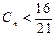 成立,若存在,求自然数
成立,若存在,求自然数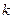 的最小值。若不存在,说明理由。
的最小值。若不存在,说明理由。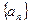 满足
满足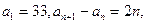 则
则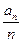 的最小值为
的最小值为 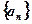
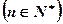 中,
中,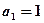 ,
,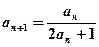 ,则
,则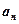 =
=