题目内容

7．已知数列{an}满足a1=3，且an+1=an+log3（1+$\frac{1}{n}$），则a9=（　　）
A．3B．4C．log310+3D．5

分析 an+1=an+log3（1+$\frac{1}{n}$），可得an+1-an=log3（n+1）-log3n，利用“累加求和”与对数的运算性质即可得出．

解答 解：∵an+1=an+log3（1+$\frac{1}{n}$），
∴an+1-an=log3（n+1）-log3n，
∴n≥2，an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1
=（log3n-log3（n-1））+（log3（n-1）-log3（n-2））+…+（log32-log31）+3
=log3n+3，
∴a9=log39+3=5，
故选：D．

点评 本题考查了“累加求和”、对数的运算性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
17．已知函数f（x）=$\frac{e}{x}$-lnx，g（x）=ex-1+a-lnx，其中e=2.71828…，a∈R．
（1）求f（x）的零点；
（2）求g（x）的极值；
（3）如果s，t，r满足|s-r|＜|t-r|，那么称s比t更靠近r．当a≥2且x≥1时，试比较$\frac{e}{x}$和ex-1+a哪个更靠近lnx，并说明理由．
18．三棱锥P-ABC中，已知∠APC=∠BPC=∠APB=$\frac{π}{3}$，点M是△ABC的重心，且$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\overrightarrow{PB}$$•\overrightarrow{PC}$+$\overrightarrow{PC}$$•\overrightarrow{PA}$=9，则|$\overrightarrow{PM}$|的最小值为（　　）
A．2$\sqrt{2}$B．$\sqrt{6}$C．$\frac{4\sqrt{3}}{3}$D．2
15．已知实数x，y满足约束条件$\left\{\begin{array}{l}x-y≥1\\ x+y≥1\\ 2x-y≤4\end{array}\right.$，则z=x+2y的最大值为7．
2．已知△ABC的外接圆半径为R，且$2R（{sin^2}A-{sin^2}C）=（\sqrt{2}a-b）sinB$（其中a，b分别是∠A，∠B的对边），那么角C的大小为（　　）
A．30°B．45°C．60°D．90°
12．如图是不锈钢保温饭盒的三视图，根据图中数据（单位：cm），求得该饭盒的表面积为900πcm2．
19．已知f（x）是定义在R上的奇函数，f（-1）=-1，且当x＞0时，有xf′（x）＞f（x），则不等式f（x）＞x的解集是（　　）
A．（-1，0）B．（1，+∞）C．（-1，0）∪（1，+∞）D．（-∞，-1）∪（1，+∞）
16．若变量x，y满足$\left\{\begin{array}{l}2x-y+2≤0\\ x+2y-4≥0\\ x-3y+11≥0\end{array}\right.$，则z=2x+y的取值范围是[-1，6]．
17．已知某几何体的三视图如图所示，则该几何体的体积为（　　）
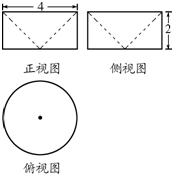
A．$\frac{8}{3}$πB．$\frac{16}{3}$πC．8πD．16π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网