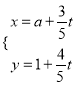题目内容
【题目】已知命题![]() 函数
函数![]() 在
在![]() 上单调递减;命题
上单调递减;命题![]() 曲线
曲线![]() 为双曲线.
为双曲线.
(Ⅰ)若“![]() 且
且![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(I)对函数![]() 求导,利用分离常数法求得命题
求导,利用分离常数法求得命题![]() 中
中![]() 的取值范围,利用双曲线的标准方程的概念求得命题
的取值范围,利用双曲线的标准方程的概念求得命题![]() 中
中![]() 的取值范围. 若“
的取值范围. 若“![]() 且
且![]() ”为真命题则
”为真命题则![]() 均为真命题,求
均为真命题,求![]() 中两个
中两个![]() 的取值范围的交集,得到题目所求
的取值范围的交集,得到题目所求![]() 的取值范围.(II)若“
的取值范围.(II)若“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 一真一假,分别根据“
一真一假,分别根据“![]() 真
真![]() 假”或者“
假”或者“![]() 假
假![]() 真”两类,结合(I)的数据,求得实数
真”两类,结合(I)的数据,求得实数![]() 的取值范围.
的取值范围.
(Ⅰ)若![]() 为真命题,
为真命题,![]() 在
在![]() 恒成立,即
恒成立,即![]() 在
在![]() 恒成立,∵
恒成立,∵![]() 在
在![]() 的最大值是3,
的最大值是3,![]()
![]() ①
①
若![]() 为真命题,则
为真命题,则![]() ,解得
,解得![]() ,②
,②
若“![]() 且
且![]() ”为真命题,即
”为真命题,即![]() ,
,![]() 均为真命题,所以
均为真命题,所以![]() ,解得
,解得![]() ,
,
综上所述,若“![]() 且
且![]() ”为真命题,则实数
”为真命题,则实数![]() 的取值范围为
的取值范围为![]() ;
;
(Ⅱ)若“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题,即
”为假命题,即![]() ,
,![]() 一真一假,
一真一假,
当![]() 真
真![]() 假时,
假时,![]() ,解得
,解得![]() ,
,
当![]() 假
假![]() 真时,
真时,![]() ,解得
,解得![]() ,
,
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目