题目内容
【题目】已知定义在
上的偶函数
和奇函数
，且
.
（1）求函数，的解析式；
（2）设函数
，记
.探究是否存在正整数
，使得对任意的
，不等式
恒成立？若存在，求出所有满足条件的正整数
的值；若不存在，请说明理由.
【答案】（1）见解析；（2）
【解析】
(1)已知
，结合函数的奇偶性可得
，解方程组即可得函数解析式；（2）由函数奇偶性的性质可知
为奇函数，图象关于
对称，则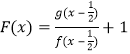
的图象关于点
中心对称，利用对称性可得
，然后利用恒成立问题解
即可.
（1）
，
函数
为偶函数，
为奇函数，
，
，
.
（2）易知为奇函数，其函数图象关于中心对称，
函数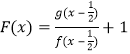的图象关于点中心对称，
即对任意的
，
成立.
，
.
两式相加，得
.
即
.
.
，即
.
.
，
恒成立.
令
，
.
则
在
上单调递增.
在
上单调递增.
.
又已知
，
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】宁德市某汽车销售中心为了了解市民购买中档轿车的意向，在市内随机抽取了100名市民为样本进行调查，他们月收入(单位：千元)的频数分布及有意向购买中档轿车人数如下表：
月收入 | [3，4) | [4，5) | [5，6) | [6，7) | [7，8) | [8，9) |
频数 | 6 | 24 | 30 | 20 | 15 | 5 |
有意向购买中档轿车人数 | 2 | 12 | 26 | 11 | 7 | 2 |
将月收入不低于6千元的人群称为“中等收入族”，月收入低于6千元的人群称为“非中等收入族”．
（Ⅰ）在样本中从月收入在[3，4)的市民中随机抽取3名，求至少有1名市民“有意向购买中档轿车”的概率.
（Ⅱ）根据已知条件完善下面的2×2列联表，并判断有多大的把握认为有意向购买中档轿车与收入高低有关？
非中等收入族 | 中等收入族 | 总计 | |||||
有意向购买中档轿车人数 | 40 | ||||||
无意向购买中档轿车人数 | 20 | ||||||
总计 | 100 | ||||||
| 0.10 | 0.05 | 0.010 | 0.005 | |||
| 2.706 | 3.841 | 6.635 | 7.879 | |||
附：
