题目内容
5.已知全集U={x|x-2≥0或x≤1},A={x|x2-4x+3>0},B=(-∞,1]∪(2,+∞),求A∩B及∁U(A∪B).分析 先求出全集U=(-∞,1]∪[2,+∞),A=(-∞,1)∪(3,+∞),然后进行交集、并集,以及补集的运算即可.
解答 解:U={x|x-2≥0或x≤1}=(-∞,1]∪[2,+∞),A={x|x2-4x+3>0}=(-∞,1)∪(3,+∞),B=(-∞,1]∪(2,+∞);
∴A∩B=(-∞,1)∪(3,+∞),A∪B=(-∞,1]∪(2,+∞),∁U(A∪B)={2}.
点评 考查描述法、列举法表示集合,以及区间表示集合,集合的交集、并集,及补集的运算.

练习册系列答案
相关题目
16.若6<a<10,$\frac{a}{2}$≤b≤2a,c=a+b,那么c的取值范围是( )
| A. | 9≤c≤18 | B. | 15<c<30 | C. | 9≤c≤30 | D. | 9<c<30 |
10.命题“若对任意?n∈N*都有an<an+1,则数列{an}是递增数列”的逆否命题是( )
| A. | 若数列{an}是递减数列,则对任意n∈N*都有an≥an+1 | |
| B. | 若数列{an}是递减数列,则存在n∈N*都有an≥an+1 | |
| C. | 若数列{an}不是递增数列,则对任意n∈N*都有an≥an+1 | |
| D. | 若数列{an}不是递增数列,则存在n∈N*都有an≥an+1 |
15.i是虚数单位,复数$\frac{i}{2+i}$=( )
| A. | $\frac{-1+2i}{3}$ | B. | $\frac{1+2i}{3}$ | C. | $\frac{1+2i}{5}$ | D. | $\frac{-1+2i}{5}$ |
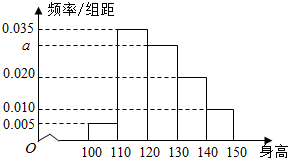 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),