题目内容
12．若直线l1：mx+8y+1=0与l2：2x+my-1=0垂直，则m的值为0．分析 根据两直线垂直，A1•A2+B1•B2=0，列出方程求出m的值．
解答 解：∵直线l1：mx+8y+1=0与l2：2x+my-1=0垂直，
∴2m+8m=0，
解得m=0．
故答案为：0．
点评 本题考查了两条直线垂直的应用问题，是基础题目．
练习册系列答案
相关题目
3．在首项为负数的等差数列{an}中，若a10+a11+a12=0，则当数列{an}的前n项和Sn取最小值时，n等于．
| A． | 10 | B． | 10或11 | C． | 11 | D． | 9或10 |
7．若f（x）=x+$\frac{1}{x}$，则下列式子中正确的是（ ）
| A． | f（-1）=0 | B． | f（0）=0 | C． | f（-x）=f（x） | D． | f（$\frac{1}{x}$）=f（x） |
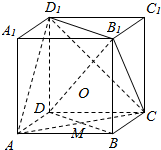如图所示，在正方体ABCD-A1B1C1D1中，B1D与平面ACD1交于点O，BD与平面ACD1交于点M，求证：M，O，D1三点共线．
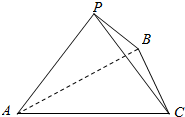如图，三棱锥P-ABC的底面是边长为2的等边三角形．若PA=PB=$\sqrt{2}$．二面角P-BA-C的大小为60°，则三棱锥P-ABC的外接球的半径=$\frac{\sqrt{13}}{3}$．