题目内容
【题目】如图：在四棱锥
中，底面
为菱形，且
， 
底面
，
， 
， 
是
上点，且
平面
.
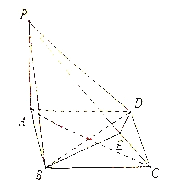
（1）求证： 
；（2）求三棱锥
的体积.
【答案】（1）见解析;（2）
.
【解析】试题分析：（1）根据菱形性质得对角线相互垂直,根据
底面
得
,再根据线面垂直判定定理得
面
即可得结果（2）记
与
的交点为
，则BD 为高,三角形POE为底,根据锥体体积公式求体积
试题解析：（1）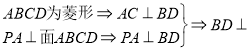
面
（2）记
与
的交点为
，连接
平面
在
中： 
， 
， 
， 
在
中： 
， 
，则
，即
，
则
【题型】解答题
【结束】
21
【题目】已知椭圆
： 
的离心率
，且其的短轴长等于
.
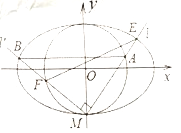
（1）求椭圆
的标准方程；
（2）如图，记圆
： 
，过定点
作相互垂直的直线
和
，直线
（斜率
）与圆
和椭圆
分别交于
、
两点，直线
与圆
和椭圆
分别交于
、
两点，若
与
面积之比等于
，求直线
的方程.
【答案】（1）
;（2）
【解析】试题分析：（1）根据题意可列关于a,b,C的方程组，解得
， 
，（2）先利用坐标表示面积之比： 
，联立直线方程与圆或椭圆方程，解得交点横坐标，代入化简可得直线斜率，即得直线
的方程.
试题解析：（1）
， 
， 
得到
， 
，椭圆
的标准方程为： 
（2）直线
的方程为： 
，联立
，得到
，
得到
，用
取代
得到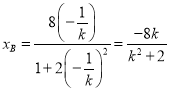
联立
，得到
，得到
用
取代
得到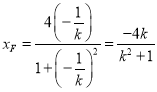
（由几何性质也知
为直径，横坐标互为相反数）
即
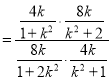
，得到
即
，直线
的方程为： 
练习册系列答案
名校课堂系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x与相应的生产能耗y的几组对照数据
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
（1）请画出上表数据的散点图;
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
.(其中
， 
).
