题目内容
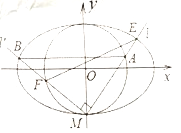
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,若抛物线
,若抛物线![]() 的焦点与椭圆的一个焦点重合.
的焦点与椭圆的一个焦点重合.
(1)求椭圆的标准方程;
(2)过椭圆的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)求出抛物线的焦点坐标,得出椭圆的焦点,根据离心率,求出![]() 的值,再算出
的值,再算出![]() ,得到椭圆的方程;(2)设A,B的横坐标分别为
,得到椭圆的方程;(2)设A,B的横坐标分别为![]() ,求出直线m的方程,联立直线和椭圆方程,由韦达定理,求出
,求出直线m的方程,联立直线和椭圆方程,由韦达定理,求出![]() ,计算出弦长
,计算出弦长![]() ,
, ![]() 到直线
到直线![]() 的距离
的距离![]() ,算出
,算出![]() 的面积。
的面积。
试题解析:(1)由题意,设所求椭圆标准方程为: ![]() ,焦距为
,焦距为![]()
∵抛物线![]() 的焦点为
的焦点为![]() ,∴
,∴![]() ,
,
又离心率![]() ,
, ![]()
再由![]() ;
;
所求椭圆标准方程为: ![]()
(2)由(1)知:左焦点为![]() ,直线m的方程为:
,直线m的方程为: ![]()
![]()
![]() ,
, ![]() ,
,
由弦长公式![]() ;
;
![]() 到直线
到直线![]() 的距离
的距离![]() ;
;
![]() 。
。

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 |
|
|
|
|
|
|
昼夜温差 |
|
|
|
|
|
|
就诊人数 |
|
|
|
| 16 |
|
该兴趣小组确定的研究方案是:先从这六组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的2组数据恰好是相邻两个月的概率;
(2)若选取的是![]() 月与
月与![]() 月的两组数据,请根据
月的两组数据,请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问(2)中所得线性回归方程是否理想?
人,则认为得到的线性回归方程是理想的,试问(2)中所得线性回归方程是否理想?
参考公式:
img src="http://thumb.zyjl.cn/questionBank/Upload/2018/08/07/18/7f4fe67a/SYS201808071848019525920497_ST/SYS201808071848019525920497_ST.020.png" width="244" height="61" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
![]()