题目内容
5．
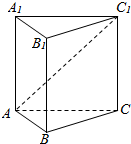如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，直线AC1与平面BCC1B1所成角的余弦值等于（ ）| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{10}}{5}$ | C． | $\frac{\sqrt{5}}{4}$ | D． | $\frac{\sqrt{10}}{4}$ |
分析 由题意，取BC的中点E，连接C1E，AE，证明AE⊥面BB1C1C，∠AC1E就是AC1与平面BB1C1C所成的角，解直角三角形AC1E即可．
解答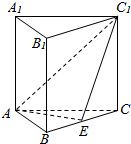 
解：取BC的中点E，连接C1E，AE
则AE⊥BC，
正三棱柱ABC-A1B1C1中，
∴面ABC⊥面BB1C1C，
面ABC∩面BB1C1C=BC，
∴AE⊥面BB1C1C，
∴∠AC1E就是AC1与平面BB1C1C所成的角，
在Rt△AC1E中，∵AB=AA1，
sin∠AC1E=$\frac{AE}{{AC}_{1}}$=$\frac{\sqrt{3}}{2\sqrt{2}}$=$\frac{\sqrt{6}}{4}$．cos∠AC1E=$\sqrt{1-（\frac{\sqrt{6}}{4}）^{2}}$=$\frac{\sqrt{10}}{4}$．
故选：D．
点评 考查直线和平面所成的角，求直线和平面所成的角关键是找到斜线在平面内的射影，把空间角转化为平面角求解，属中档题．
练习册系列答案
小学课时特训系列答案
相关题目
13．cos20°+cos60°+cos100°+cos140°的为（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |