题目内容
14.在平面直角坐标系xOy中,已知点P在曲线xy=1(x>0)上,点P在x轴上的射影为M.若点P在直线x-y=0的下方,则$\frac{O{P}^{2}}{OM-MP}$的最小值为2$\sqrt{2}$.分析 设点P(t,$\frac{1}{t}$),将$\frac{O{P}^{2}}{OM-MP}$化成关于t的表达式,结合题意得t-$\frac{1}{t}$是正数,利用基本不等式可求出$\frac{O{P}^{2}}{OM-MP}$的最小值即可.
解答 解:设点P(t,$\frac{1}{t}$),得OP2=t2+$\frac{1}{{t}^{2}}$,而OM=t,MP=$\frac{1}{t}$,
∴$\frac{O{P}^{2}}{OM-MP}$=$\frac{{t}^{2}+\frac{1}{{t}^{2}}}{t-\frac{1}{t}}$=$\frac{{(t-\frac{1}{t})}^{2}+2}{t-\frac{1}{t}}$=(t-$\frac{1}{t}$)+$\frac{2}{t-\frac{1}{t}}$,
∵点P在直线x-y=0的下方,且t>0
∴t>1,得t-$\frac{1}{t}$是正数,所以(t-$\frac{1}{t}$)+$\frac{2}{t-\frac{1}{t}}$≥2$\sqrt{2}$,
故答案为:$2\sqrt{2}$.
点评 本题通过曲线上一个动点,求关于线段OP、OM、MP的分式的最小值,着重考查了曲线与方程、利用基本不等式求最值和简单的演绎推理等知识,属于中档题.

练习册系列答案
相关题目
5.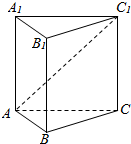 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )
 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{10}}{4}$ |
9.四棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为( )
| A. | 6cm2 | B. | $\frac{{3\sqrt{5}}}{4}$cm2 | C. | $\frac{2}{3}$$\sqrt{3}$cm2 | D. | 3$\sqrt{5}$cm2 |
4. 运行如图的程序,若x=1,则输出的y等于( )
运行如图的程序,若x=1,则输出的y等于( )
 运行如图的程序,若x=1,则输出的y等于( )
运行如图的程序,若x=1,则输出的y等于( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |