题目内容
17.在平面直角坐标系xoy中,已知直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=4-2t}\end{array}\right.$(参数t∈R),同时,在以坐标原点为极点,x轴的正半轴为极轴建立的极坐标系中,圆C的极坐标方程为ρ=4cosθ(θ为参数)(1)求圆C的直角坐标方程.
(2)求直线l被圆C所截得的弦长.
分析 (1)利用极坐标与直角坐标互化,求解圆C的直角坐标方程.
(2)求出直线的普通方程,然后求出圆心到直线的距离,利用垂径定理求解即可.
解答 解:(1)圆C的极坐标方程为ρ=4cosθ(θ为参数)
可得ρ2=4ρcosθ,可得圆的普通方程为:x2+y2=4x,即(x-2)2+y2=4.
(2)直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=4-2t}\end{array}\right.$(参数t∈R),消去参数t,可得2x+y=6.
圆的圆心(2,0),半径为:2,圆心到直线的距离为:$\frac{|4-6|}{\sqrt{5}}$=$\frac{2}{\sqrt{5}}$,
直线l被圆C所截得的弦长:2$\sqrt{{2}^{2}-{(\frac{2}{\sqrt{5}})}^{2}}$=$2\sqrt{4-\frac{4}{5}}$=$\frac{8\sqrt{5}}{5}$.
点评 本题考查参数方程以及极坐标方程与普通方程的互化,直线与圆的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
3.若平面α∥平面β,l?α,则l与β的位置关系是( )
| A. | l与β相交 | B. | l与β平行 | C. | l在β内 | D. | 无法判定 |
5.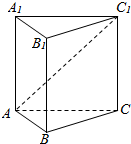 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )
 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{10}}{4}$ |
9.四棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为( )
| A. | 6cm2 | B. | $\frac{{3\sqrt{5}}}{4}$cm2 | C. | $\frac{2}{3}$$\sqrt{3}$cm2 | D. | 3$\sqrt{5}$cm2 |
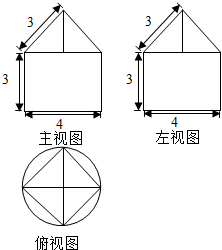 一个空间几何体的三视图如图所示,根据图中数据:
一个空间几何体的三视图如图所示,根据图中数据: