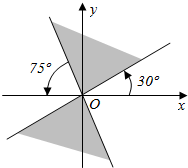
题目内容
11．过点（2，-4），且倾斜角的余弦值为-$\frac{3}{5}$的直线方程为4x+3y+4=0．分析 利用同角三角函数基本关系式可得斜率，再利用点斜式即可得出．
解答 解：设直线的倾斜角为θ，θ∈[0，π）．
∵cosθ=-$\frac{3}{5}$，
∴sinθ=$\frac{4}{5}$，tanθ=-$\frac{4}{3}$．
∴要求的直线方程为：y+4=-$\frac{4}{3}$（x-2），化为4x+3y+4=0．
故答案为：4x+3y+4=0．
点评 本题考查了同角三角函数基本关系式、斜率、点斜式，考查了计算能力，属于基础题．
练习册系列答案
相关题目
3．若平面α∥平面β，l?α，则l与β的位置关系是（ ）
| A． | l与β相交 | B． | l与β平行 | C． | l在β内 | D． | 无法判定 |
5．
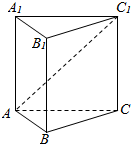如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，直线AC1与平面BCC1B1所成角的余弦值等于（ ）
如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，直线AC1与平面BCC1B1所成角的余弦值等于（ ）| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{10}}{5}$ | C． | $\frac{\sqrt{5}}{4}$ | D． | $\frac{\sqrt{10}}{4}$ |