题目内容
15.已知数列{an}满足:a1=1,n∈N*.(1)若an+1=2an+n+1,求数列的通项an.
(2)若an+1=2an+4n+2,求数列的通项an.
(3)若an+1=$\frac{{a}_{n}}{-7{a}_{n}-6}$,求数列的通项an.
(4)若an+1=an2+2an,求数列的通项an.
分析 (1)由原递推式变形可得an+1+n+3=2(an+n+2),则数列{an+n+2}是以a1+1+2=4为首项,以2为公比的等比数列,由等比数列的通项公式可求数列的通项an;
(2)把已知递推式两边同时除以2n+1,然后分别取n=1、2、…、n-1,再利用累加法,分组后由等比数列的前n项和即可求得答案;
(3)把已知递推式两边取倒数,然后构造等比数列{$\frac{1}{{a}_{n}}+1$},求其通项公式后可得数列的通项an;
(4)由已知递推式可得${a}_{n+1}+1=({a}_{n}+1)^{2}$,两边取对数得lg(an+1+1)=2lg(an+1),可得数列{lg(an+1)}是以lg2为首项,以2为公比的等比数列,求其通项公式后可得数列的通项an.
解答 解:a1=1,
(1)由an+1=2an+n+1,得an+1+n+3=2(an+n+2),
∴数列{an+n+2}是以a1+1+2=4为首项,以2为公比的等比数列,
则an+n+2=4×2n-1=2n+1,
∴${a}_{n}={2}^{n+1}-n-2$;
(2)由an+1=2an+4n+2,得$\frac{{a}_{n+1}}{{2}^{n+1}}=\frac{{a}_{n}}{{2}^{n}}+{2}^{n-1}+\frac{1}{{2}^{n}}$,
∴$\frac{{a}_{2}}{{2}^{2}}=\frac{{a}_{1}}{{2}^{1}}+{2}^{0}+\frac{1}{2}$,$\frac{{a}_{3}}{{2}^{3}}=\frac{{a}_{2}}{{2}^{2}}+{2}^{1}+\frac{1}{{2}^{2}}$,$\frac{{a}_{4}}{{2}^{4}}=\frac{{a}_{3}}{{2}^{3}}+{2}^{2}+\frac{1}{{2}^{3}}$,
…
$\frac{{a}_{n}}{{2}^{n}}=\frac{{a}_{n-1}}{{2}^{n-1}}+{2}^{n-2}+\frac{1}{{2}^{n-1}}$,
累加得:$\frac{{a}_{n}}{{2}^{n}}=\frac{1}{2}+({2}^{0}+{2}^{1}+…+{2}^{n-2})+(\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}})$
=$\frac{1}{2}+\frac{1×(1-{2}^{n-1})}{1-2}+\frac{\frac{1}{2}×(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$=${2}^{n-1}+\frac{1}{{2}^{n-1}}+\frac{1}{2}$,
∴${a}_{n}={2}^{2n-1}+{2}^{n-1}-2$;
(3)由an+1=$\frac{{a}_{n}}{-7{a}_{n}-6}$,得$\frac{1}{{a}_{n+1}}=-\frac{6}{{a}_{n}}-7$,
即$\frac{1}{{a}_{n+1}}+1=-6(\frac{1}{{a}_{n}}+1)$,
∵$\frac{1}{{a}_{1}}+1=2≠0$,
∴数列{$\frac{1}{{a}_{n}}+1$}构成以2为首项,以-6为公比的等比数列,
则$\frac{1}{{a}_{n}}+1=2×(-6)^{n-1}$,
∴$\frac{1}{{a}_{n}}=2×(-6)^{n-1}-1$,则${a}_{n}=\frac{1}{2×(-6)^{n-1}-1}$;
(4)由an+1=an2+2an,得${a}_{n+1}+1=({a}_{n}+1)^{2}$,
两边取对数得lg(an+1+1)=2lg(an+1),
∵lg(a1+1)=lg2≠0,
∴数列{lg(an+1)}是以lg2为首项,以2为公比的等比数列,
则$lg({a}_{n}+1)={2}^{n-1}lg2$,
∴${a}_{n}+1=1{0}^{{2}^{n-1}lg2}$,则${a}_{n}=1{0}^{{2}^{n-1}lg2}-1$.
点评 本题考查数列递推式,训练了由数列递推式构造等比数列求数列的通项公式,考查了累积法求数列的通项公式,属中档题.

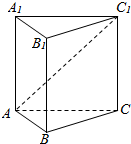 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{10}}{4}$ |
 运行如图的程序,若x=1,则输出的y等于( )
运行如图的程序,若x=1,则输出的y等于( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
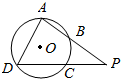 如图,四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点P,若$\frac{PB}{PA}$=$\frac{1}{2}$,$\frac{PC}{PD}$=$\frac{1}{3}$,则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$.
如图,四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点P,若$\frac{PB}{PA}$=$\frac{1}{2}$,$\frac{PC}{PD}$=$\frac{1}{3}$,则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$.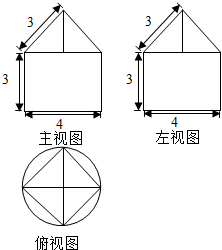 一个空间几何体的三视图如图所示,根据图中数据:
一个空间几何体的三视图如图所示,根据图中数据: