题目内容
设函数f(x)＝
sinxcosx＋cos2x＋a.
(1)写出函数f(x)的最小正周期及单调递减区间；
(2)当x∈
时，函数f(x)的最大值与最小值的和为
，求a的值．
sinxcosx＋cos2x＋a.(1)写出函数f(x)的最小正周期及单调递减区间；
(2)当x∈
时，函数f(x)的最大值与最小值的和为，求a的值．（1）
（2）a＝0
（2）a＝0(1)f(x)＝
sin2x＋
＋a＝sin
＋a＋
，∴T＝π.由
＋2kπ≤2x＋
≤
＋2kπ，得＋kx≤x≤
＋kπ.故函数f(x)的单调递减区间是(k∈Z)．
(2)∵－≤x≤
，∴－≤2x＋≤
.∴－≤sin≤1.当x∈时，原函数的最大值与最小值的和为
＝，∴a＝0
sin2x＋＋a＝sin＋a＋，∴T＝π.由＋2kπ≤2x＋≤＋2kπ，得＋kx≤x≤＋kπ.故函数f(x)的单调递减区间是(k∈Z)．(2)∵－
≤x≤，∴－≤2x＋≤.∴－≤sin≤1.当x∈时，原函数的最大值与最小值的和为＝，∴a＝0
练习册系列答案
智慧小复习系列答案
相关题目
，若a、b、c互不相等，且
，则a＋b＋c的取值范围是（ ）
,则函数g(x)=asinx+cosx的最大值是( )
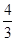
,-1]
cos
的最小正周期为________．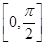
时，求函数f(x)的最大值和最小值．
－cos2x·cos
在
上的单调递增区间为_________．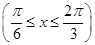
的值域是________．
-φ)-sin(
,0)对称,且在区间[0,