题目内容
函数y=sin2x+sinx-1的值域为( )
| A.[-1,1] | B.[- ,-1] ,-1] |
C.[- ,1] ,1] | D.[-1, ] ] |
C
令sinx=t,则t∈[-1,1],
可得y=t2+t-1=(t+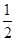 )2-
)2- ,
,
故y∈[- ,1].
,1].
故选C.
可得y=t2+t-1=(t+
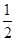 )2-
)2- ,
,故y∈[-
 ,1].
,1].故选C.

练习册系列答案
相关题目
题目内容
| A.[-1,1] | B.[- ,-1] ,-1] |
C.[- ,1] ,1] | D.[-1, ] ] |
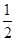 )2-
)2- ,
, ,1].
,1].