题目内容
2.若“x∈[-2,1]”是“x∈{x|x2-ax-4≤0|≤0}”的充分但不必要条件,则实数a的取值范围是[-3,0]•分析 由x2-ax-4≤0,解得$\frac{a-\sqrt{{a}^{2}+16}}{2}$≤x≤$\frac{a+\sqrt{{a}^{2}+16}}{2}$,根据“x∈[-2,1]”是“x∈{x|x2-ax-4≤0|≤0}”的充分但不必要条件,可得$\left\{\begin{array}{l}{\frac{a-\sqrt{{a}^{2}+16}}{2}≤-2}\\{1≤\frac{a+\sqrt{{a}^{2}+16}}{2}}\end{array}\right.$,且等号不能同时成立.解出即可.
解答 解:由x2-ax-4≤0,解得$\frac{a-\sqrt{{a}^{2}+16}}{2}$≤x≤$\frac{a+\sqrt{{a}^{2}+16}}{2}$,
∵“x∈[-2,1]”是“x∈{x|x2-ax-4≤0|≤0}”的充分但不必要条件,
∴$\left\{\begin{array}{l}{\frac{a-\sqrt{{a}^{2}+16}}{2}≤-2}\\{1≤\frac{a+\sqrt{{a}^{2}+16}}{2}}\end{array}\right.$,且等号不能同时成立.
化为$\left\{\begin{array}{l}{a+4≤\sqrt{{a}^{2}+16}}\\{2≤a+\sqrt{{a}^{2}+16}}\end{array}\right.$,
当a>0时,$a+4≤\sqrt{{a}^{2}+16}$不成立;
∴a≤0,∴(2-a)2≤a2+16,解得a≥-3,因此-3≤a≤0,
经过验证满足条件.
∴实数a的取值范围是[-3,0].
故答案为:[-3,0].
点评 本题考查了简易逻辑的判定方法、一元二次不等式与根式不等式的解法、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案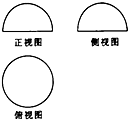
| A. | 半球 | B. | 球 | C. | 圆柱 | D. | 圆锥 |
 如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )
如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )| A. | $\frac{8}{3}$π | B. | $\frac{7}{3}$π | C. | 2π | D. | $\frac{5}{3}$π |
| A. | $\frac{32}{3}$(1-4-n) | B. | $\frac{32}{3}$(1-2-n) | C. | 16(1-4-n) | D. | 16(1-2-n) |