题目内容
提高过江大桥的车辆通行能力可改善整个城市的交通状况。在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数。当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
(Ⅰ)函数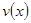 的表达式为
的表达式为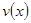 =
= ;(Ⅱ)当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
;(Ⅱ)当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
解析试题分析:(1)由车流密度不超过20辆/千米时,车流速度为60千米/小时,可得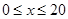 时,
时,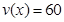 ;又
;又 时,车流速度
时,车流速度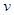 是车流密度
是车流密度 的一次函数,设
的一次函数,设 ,利用
,利用 时
时 及
及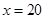 时
时 可求出
可求出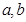 ,据此可求
,据此可求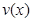 表达式.(2)
表达式.(2)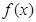 是关于
是关于 的分段函数,求出每段的最大值,再比较可得
的分段函数,求出每段的最大值,再比较可得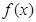 的最大值.
的最大值.
试题解析:(Ⅰ)由题意:当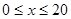 时,
时,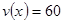 ;当
;当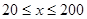 时,设
时,设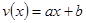 ,显然
,显然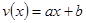 在
在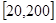 是减函数,由已知得
是减函数,由已知得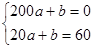 ,解得
,解得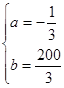
故函数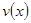 的表达式为
的表达式为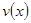 =
=
(Ⅱ)依题意并由(Ⅰ)可得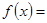

当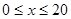 时,
时,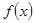 为增函数,故当
为增函数,故当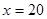 时,其最大值为
时,其最大值为 ;
;
当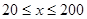 时,
时, ,
,
当且仅当 ,即
,即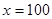 时,等号成立.
时,等号成立.
所以,当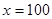 时,
时,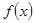 在区间
在区间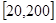 上取得最大值
上取得最大值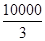 .
.
综上,当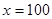 时,
时,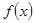 在区间
在区间 上取得最大值
上取得最大值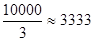 ,
,
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
考点:1.函数的实际应用;2.函数的最值求法;3.均值不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
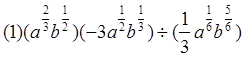
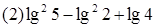
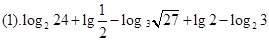
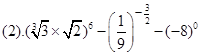
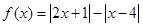 .
.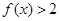 ;
;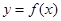 的最小值.
的最小值.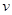 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当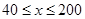 时,车流速度
时,车流速度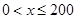 时,求函数
时,求函数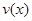 的表达式;
的表达式;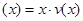 ,
,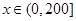 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.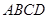 和分别以
和分别以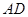 、
、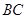 为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,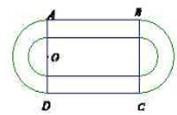
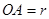 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积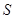 与
与 的函数关系式
的函数关系式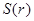 ;
;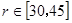 ,问当
,问当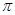 取3近似计算).
取3近似计算). (m∈N+)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足
(m∈N+)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足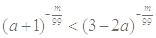 的a的取值范围.
的a的取值范围. ;
;