题目内容
如图是某重点中学学校运动场平面图,运动场总面积15000平方米,运动场是由一个矩形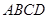 和分别以
和分别以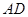 、
、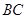 为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,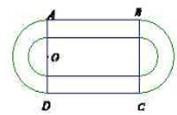
(Ⅰ)设半圆的半径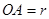 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积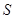 与
与 的函数关系式
的函数关系式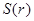 ;
;
(Ⅱ)由于受运动场两侧看台限制, 的范围为
的范围为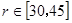 ,问当
,问当 为何值时,运动场造价最低(第2问
为何值时,运动场造价最低(第2问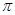 取3近似计算).
取3近似计算).
(Ⅰ)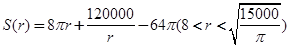 ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)塑胶跑道由两个半圆和两个矩形构成,利用圆和矩形的面积公式便可得其面积.
(Ⅱ)单位造价乘以面积便得总造价,这样可得总造价与半径的关系式: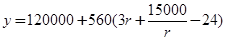 ,这个式子可用重要不等式求其最小值及相应的半径.
,这个式子可用重要不等式求其最小值及相应的半径.
试题解析:(Ⅰ)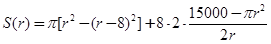
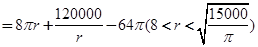 5分
5分
(Ⅱ)总造价: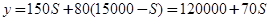
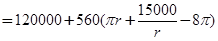
 8分
8分
令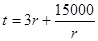 ,则
,则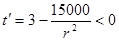
∴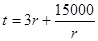 在区间
在区间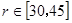 上单调递减
上单调递减
故当 时,总造价最低. 12分
时,总造价最低. 12分
考点:1、函数的应用;2、重要不等式.

练习册系列答案
相关题目
 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
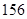 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?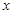 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为 (单位:厘米),已知当
(单位:厘米),已知当 时,
时,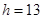 .试将
.试将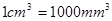 )
) 满足
满足 ,且
,且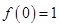 。
。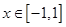 时,方程
时,方程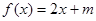 有解,求实数
有解,求实数 的取值范围;
的取值范围;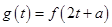 ,
,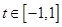 ,求
,求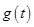 的最大值.
的最大值. 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数. 时,求函数
时,求函数 的表达式;
的表达式; 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时). 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度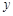 (克/升)随着时间
(克/升)随着时间 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为 ,其中
,其中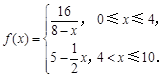 若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.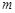 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求
 在[-3,2]上具有单调性,求实数
在[-3,2]上具有单调性,求实数 的取值范围。
的取值范围。 有最小值为-12,求实数
有最小值为-12,求实数 ,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1). (其中
(其中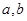 为常数且
为常数且  )的图象经过点
)的图象经过点 .
. 的解析式;
的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. 的解集为M.
的解集为M. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数