题目内容
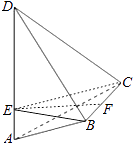
【题目】如图，AD与BC是四面体ABCD中互相垂直的棱，BC=2，若AD=2c，且AB+BD=AC+CD=2a，其中a、c为常数，则四面体ABCD的体积的最大值是 ． 
【答案】
【解析】解：作BE⊥AD于E，连接CE，则AD⊥平面BEC，所以CE⊥AD，
由题设，B与C都是在以AD为焦点的椭球上，且BE、CE都垂直于焦距AD，
AB+BD=AC+CD=2a，显然△ABD≌△ACD，所以BE=CE．
取BC中点F，∴EF⊥BC，EF⊥AD，要求四面体ABCD的体积的最大值，因为AD是定值，只需三角形EBC的面积最大，因为BC是定值，所以只需EF最大即可，
当△ABD是等腰直角三角形时几何体的体积最大，∵AB+BD=AC+CD=2a，
∴AB=a，所以EB= 
，EF= 
，
所以几何体的体积为： 
× 
= ．
所以答案是： ．
练习册系列答案
相关题目
【题目】食品安全一直是人们关心和重视的问题，学校的食品安全更是社会关注的焦点.某中学为了加强食品安全教育，随机询问了36名不同性别的中学生在购买食品时是否看保质期，得到如下“性别”与“是否看保质期”的列联表：
男 | 女 | 总计 | |
看保质期 | 8 | 22 | |
不看保持期 | 4 | 14 | |
总计 |
（1）请将列联表填写完整，并根据所填的列联表判断，能否有
的把握认为“性别”与“是否看保质期”有关？
（2）从被询问的14名不看保质期的中学生中，随机抽取3名，求抽到女生人数
的分布列和数学期望.
附：
，（
）.
临界值表：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
