Question

【题目】如图．在四棱锥中，，，平面ABCD，且．，，M、N分别为棱PC，PB的中点.

（1）证明：A，D，M，N四点共面，且平面ADMN；

（2）求直线BD与平面ADMN所成角的正弦值．

Answer 1

【答案】(1) 证明见解析；(2)

【解析】

（1）先证，再证，即可得证；要证平面ADMN，可通过求证PB垂直于ADMN中的两条交线来证明

（2）求直线BD与平面ADMN所成角，需要找出BD在平面ADMN的射影，可通过三垂线定理去进行证明

解：（1）证明因为M，N分别为PC，PB的中点，所以；

又因为，所以．从而A，D，M，N四点共面；

因为平面ABCD，平面ABCD．所以，

又因为，，所以平面PAB，从而，

因为，且N为PB的中点，所以；

又因为，所以平面ADMN；

（2）如图，连结DN；

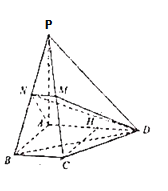
由（1）知平面ADMN，

所以，DN为直线BD在平面ADMN内的射影，且，

所以，即为直线BD与平面ADMN所成的角：

在直角梯形ABCD内，过C作于H，则四边形ABCH为矩形；

，在中，；

所以，，，

在中，，，，

所以.

综上，直线BD与平面ADMN所成角的正弦值为.