题目内容
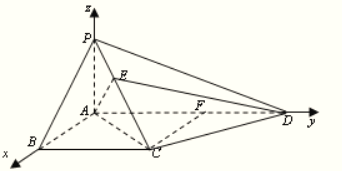
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.

(Ⅰ)求证:![]() ;
;
(Ⅱ)是否存在实数![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(1)由边长和勾股定理得![]() ,又平面
,又平面![]() 平面
平面![]() ,由定理证得
,由定理证得![]() 平面
平面![]()
![]() (2) 建立空间直角坐标系, 得出平面
(2) 建立空间直角坐标系, 得出平面![]() 的一个法向量为
的一个法向量为
![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,由题意计算得出结果
,由题意计算得出结果
解析:(Ⅰ)过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,
![]() ,
,![]() ,
,![]()
![]() 四边形
四边形![]() 为正方形,且
为正方形,且![]() ,
,![]()
在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]()
![]()
![]()
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ,且
,且![]()
![]() 平面
平面![]()
![]()
(Ⅱ)![]()
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() 平面
平面![]()
![]() ,
,![]()
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线为坐标轴建立空间直角坐标系,
所在直线为坐标轴建立空间直角坐标系,
![]()
假设存在实数![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ,令
,令![]()
![]() 点
点![]() 在棱
在棱![]() 上,
上,![]()
设![]()
![]() 则
则![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 的一个法向量为
的一个法向量为![]()
设平面![]() 的一个法向量为
的一个法向量为![]()
由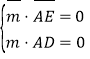 得
得![]() 令
令![]() 得
得![]()
取![]()
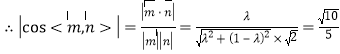
化简得![]() 又
又![]()
![]()
![]() 存在实数
存在实数![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
