题目内容
【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的一段图象如图所示．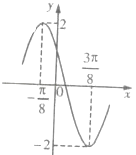 
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调增区间；
（3）求函数f（x）在[﹣ 
， 
]上的单调减区间．
【答案】
（1）解：由题意知： 
，∴ 
，
又 
，∴ 
（k∈Z）， 
（k∈Z），又|φ|＜π，∴ 
．
∴函数f（x）的解析式： 
（2）解：由 
，k∈Z，得 
，
所以f（x）的增区间为 
，k∈Z
（3）解：再根据x∈[﹣ 
， 
]，可得函数f（x）在[﹣ ， ]上的单调减区间为[﹣ 
， ]．
【解析】（1）由图象相邻的最高点和最低点的横坐标之差可求最小正周期，最高点纵坐标可求得振幅，将最高点代入解析式中求初相，可得函数的解析式（2）正弦函数的单调增区间为 
，所以可令 
，由此解出x的范围，即为要求的f（x）的单调增区间．（3）由（2）结合x∈[﹣ ， ]，可得函数f（x）在[﹣ ， ]上的单调减区间．
练习册系列答案
相关题目
