题目内容
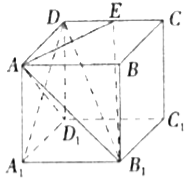
【题目】如图，棱柱ABC﹣A1B1C1的侧面BCC1B1是菱形，B1C⊥A1B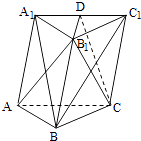 
（1）证明：平面AB1C⊥平面A1BC1；
（2）设D是A1C1上的点，且A1B∥平面B1CD，求A1D：DC1的值．
【答案】
（1）证明：因为侧面BCC1B1是菱形，所以B1C⊥BC1
又已知B1C⊥A1B，且A1B∩BC1=B，
又B1C⊥平面A1BC1，又B1C平面AB1C，
所以平面AB1C⊥平面A1BC1．
（2）解：设BC1交B1C于点E，连接DE，
则DE是平面A1BC1与平面B1CD的交线，
因为A1B∥平面B1CD，所以A1B∥DE．
又E是BC1的中点，所以D为A1C1的中点．
即A1D：DC1=1．
【解析】（1）证明平面AB1C内的直线B1C垂直平面A1BC1 ， 内的两条相交直线A1B，BC1 ， 即可证明平面AB1C⊥平面A1BC1；（2）D是A1C1上的点，且A1B∥平面B1CD，BC1交B1C于点E，连接DE，E是BC1的中点，推出D为A1C1的中点，可得A1D：DC1的值．
【考点精析】认真审题，首先需要了解直线与平面平行的性质(一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行)，还要掌握平面与平面垂直的判定(一个平面过另一个平面的垂线，则这两个平面垂直)的相关知识才是答题的关键．
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案【题目】随着人口老龄化的到来，我国的劳动力人口在不断减少，“延迟退休”已经成为人们越来越关注的话题，为了解公众对“延迟退休”的态度，某校课外研究性学习小组在某社区随机抽取了50人进行调查，将调查情况进行整理后制成下表：
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在［25,30),[55,60）的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人，进行跟踪调查．
（I）求年龄在［25,30）的被调查者中选取的2人都赞成“延迟退休”的概率；
（II）若选中的4人中，不赞成“延迟退休”的人数为
，求随机变量
的分布列和数学期望．
