题目内容
11.已知向量$\overrightarrow{a}$=(cos$\frac{3}{2}$x,sin$\frac{3}{2}$x),$\overrightarrow{b}$=(cos$\frac{x}{2}$,sin$\frac{x}{2}$),且x∈[0,$\frac{2π}{3}$].(1)求$\overrightarrow{a}$•$\overrightarrow{b}$及|$\overrightarrow{a}$+$\overrightarrow{b}$|;
(2)若f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为-$\frac{3}{2}$,求实数λ的值.
分析 (1)通过数量积,即模的运算再利用两角和公式和二倍角公式化简整理即可;
(2)先求出函数f(x)的表达式,再根据x的范围,进而利用二次的单调性求得函数的最值,问题得以解决.
解答 解:(1)$\overrightarrow{a}$=(cos$\frac{3}{2}$x,sin$\frac{3}{2}$x),$\overrightarrow{b}$=(cos$\frac{x}{2}$,sin$\frac{x}{2}$),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=cos$\frac{3}{2}$xcos$\frac{x}{2}$+sin$\frac{3}{2}$xsin$\frac{x}{2}$=cosx,
|$\overrightarrow{a}$+$\overrightarrow{b}$|2=(cos$\frac{3}{2}$x+cos$\frac{x}{2}$)2+(sin$\frac{3}{2}$x+sin$\frac{x}{2}$)2=2+2cosx=4cos2$\frac{x}{2}$,
∵x∈[0,$\frac{2π}{3}$].
∴cos$\frac{x}{2}$>0,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=2cos$\frac{x}{2}$;
(2)由(1)有f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|=cosx-4λcos$\frac{x}{2}$=2cos2$\frac{x}{2}$-4λcos$\frac{x}{2}$-1=2(cos$\frac{x}{2}$-λ)2-1-2λ2,
∵x∈[0,$\frac{2π}{3}$],
∴$\frac{x}{2}$∈[0,$\frac{π}{3}$],
∴cos$\frac{x}{2}$∈[$\frac{1}{2}$,1],
当λ<$\frac{1}{2}$时,当且仅当cos$\frac{x}{2}$=$\frac{1}{2}$时,fmin(x)=2×$\frac{1}{4}$-4λ×$\frac{1}{2}$-1=-$\frac{3}{2}$,解得λ=$\frac{1}{2}$(舍);
当$\frac{1}{2}$≤λ≤1时,当且仅当cos$\frac{x}{2}$=λ时,fmin(x)=-1-2λ2=-$\frac{3}{2}$,解得λ=$\frac{1}{2}$或λ=$-\frac{1}{2}$(舍);
当λ>1时,当且仅当cos$\frac{x}{2}$=1时,fmin(x)=2-4λ-1=-$\frac{3}{2}$,解得λ=$\frac{5}{8}$(舍);
综上所述,λ=$\frac{1}{2}$.
点评 本题主要考查了二次函数的最值,和两角和公式,二倍角公式的运用.三角函数的基本公式较多,注意多积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
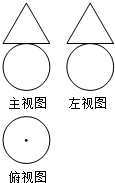 某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )| A. | $\frac{4+\sqrt{3}}{3}$π | B. | 5π | C. | 6π | D. | 7π |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | π |
| A. | -2 | B. | 2 | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |