题目内容
8.(1)已知数列{an}的前n项和为Sn,若${S_n}={3^n}+2n+1$,求an(2)等差数列{an}的前n项和记为Sn,已知a10=30,a20=50,Sn=242,求n.
分析 (1)利用递推式即可得出;
(2)利用等差数列的通项公式及其前n项和公式即可得出.
解答 解:(1)当n=1时,a1=s1=6;
当n≥2时,${a_n}={s_n}-{s_{n-1}}=({3^n}+2n+1)-[{3^{n-1}}+2(n-1)+1]=2•{3^{n-1}}+2$
由于a1不适合此式,
∴${a_n}=\left\{\begin{array}{l}6,n=1\\ 2•{3^{n-1}}+2,n≥2\end{array}\right.$.
(2)解 由an=a1+(n-1)d,a10=30,a20=50,
得程组$\left\{\begin{array}{l}{a_1}+9d=30\\{a_1}+19d=50\end{array}\right.$,
解得$\left\{\begin{array}{l}{a_1}=12\\ d=2\end{array}\right.$.
∴an=2n+10.
${s_n}=n{a_1}+\frac{n(n-1)}{2}d,{s_n}=242$,
得$12n+\frac{n(n-1)}{2}×2=242$,
解得n=11或n=-22(舍去).
∴n=11.
点评 本题考查了递推式的应用、等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19.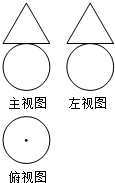 某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
 某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )| A. | $\frac{4+\sqrt{3}}{3}$π | B. | 5π | C. | 6π | D. | 7π |
16.若f(x)=sin(2x+φ)为偶函数,则φ值可能是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | π |
3.若曲线y=e-ax+1在点(0,2)处的切线与直线x+2y-1=0垂直,则a=( )
| A. | -2 | B. | 2 | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |