题目内容
【题目】全民健身旨在全面提高国民体质和健康水平，倡导全民做到每天参加一次以上的健身活动，学会两种以上健身方法，每年进行一次体质测定．为响应全民健身号召，某单位在职工体测后就某项健康指数（百分制）随机抽取了30名职工的体测数据作为样本进行调查，具体数据如茎叶图所示，其中有1名女职工的健康指数的数据模糊不清（用x表示），已知这30名职工的健康指数的平均数为76.2．
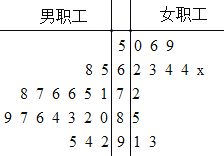
（1）根据茎叶图，求样本中男职工健康指数的众数和中位数；
（2）根据茎叶图，按男女用分层抽样从这30名职工中随机抽取5人，再从抽取的5人中随机抽取2人，求抽取的2人都是男职工的概率；
（3）经计算，样本中男职工健康指数的平均数为81，女职工现有数据（即剔除x）健康指数的平均数为69，方差为190，求样本中所有女职工的健康指数的平均数和方差（结果精确到0.1）．
【答案】（1）众数是76，中位数是81；（2）
；（3）平均数为69，方差约为174.2．
【解析】
（1）根据茎叶图中数据，计算样本中男职工健康指数的众数和中位数即可；
（2）根据分层抽样原理求出抽取的男、女职工人数，用列举法求出基本事件数，计算所求的概率值即可；
（3）根据题意求出x的值，再计算健康指数的平均数和方差．
（1）根据茎叶图，得到样本中男职工健康指数的众数是
，
中位数是
；
（2）根据茎叶图，按男女用分层抽样从这
名职工中随机抽取
人，
抽样比
男职工抽
（人），记为
，女职工
人，记为
，
从这人中随机抽取人，所有的基本事件是
、
、
、
、
、
、
、
、
、
共
种，
抽取的人都是男职工的事件为、、，
故所求的概率为P
；
（3）由题意知: 
，解得
；
所以样本中所有女职工的健康指数平均数为
，
方差为
.
练习册系列答案
阅读快车系列答案
相关题目
