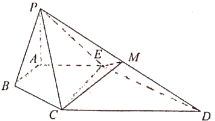
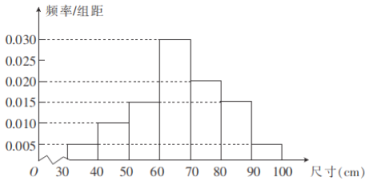
题目内容
【题目】已知数列{an}是单调递增的等差数列,a2+a4=14且a2﹣1,a3+1,a4+7成等比数列.
(1)求数列{an}的通项公式;
(2)设数列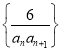 的前n项和为Sn.
的前n项和为Sn.
【答案】(1)an=3+2(n﹣1)=2n+1,n∈N*;(2)![]() .
.
【解析】
(1)设数列{an}的公差为d,d>0,由等差数列的通项公式和等比数列的中项性质,解方程可得公差和首项,进而得到所求通项公式;
(2)求得![]() 3(
3(![]() ),由数列的裂项相消求和,化简计算可得所求和.
),由数列的裂项相消求和,化简计算可得所求和.
解:(1)设数列{an}的公差为d,
由a2+a4=14,得2a3=14,即a3=7.
由a2﹣1,a3+1,a4+7成等比数列,得(a3+1)2=(a2﹣1)(a4+7),即(7+1)2=(6﹣d)(14+d),
解得d=2或d=﹣10.
又数列{an}是单调递增的等差数列,故d>0,则d=2,a1=3,
数列{an}的通项公式为an=3+2(n﹣1)=2n+1,n∈N*;
(2)![]() 3(
3(![]() ),
),
可得Sn=3(![]() )=3(
)=3(![]() )
)![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价![]() (单位:元/件)及相应月销量
(单位:元/件)及相应月销量![]() (单位:万件),对近5个月的月销售单价
(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下表数据:
的数据进行了统计,得到如下表数据:
月销售单价 | 9 |
| 10 |
| 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)该公司开展促销活动,当该产品月销售单价为7元/件时,其月销售量达到18万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() 万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
(Ⅲ)根据(Ⅰ)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中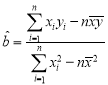 ,
,![]() .
.
参考数据:![]() ,
,