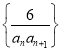题目内容
【题目】在平面直角坐标系xOy中,点P(x0,y0)在曲线y=x2(x>0)上.已知A(0,-1),![]() ,n∈N*.记直线APn的斜率为kn.
,n∈N*.记直线APn的斜率为kn.
(1)若k1=2,求P1的坐标;
(2)若k1为偶数,求证:kn为偶数.
【答案】(1)(1,1)(2)详见解析
【解析】
试题(1)由两点间斜率公式得![]() ,解方程得P1的坐标(2)先求出kn=
,解方程得P1的坐标(2)先求出kn=![]() ,再利用k1为偶数表示x0,设k1=2p(p
,再利用k1为偶数表示x0,设k1=2p(p![]() N*),则x0=p±
N*),则x0=p±![]() .最后利用二项式展开定理证明kn为偶数
.最后利用二项式展开定理证明kn为偶数
试题解析:解:(1)因为k1=2,所以![]() ,
,
解得x0=1,y0=1,所以P1的坐标为(1,1).
(2)设k1=2p(p![]() N*),即
N*),即![]() ,
,
所以![]() -2px0+1=0,所以x0=p±
-2px0+1=0,所以x0=p±![]() .
.
因为y0=x02,所以kn=![]()
所以当x0=p+![]() 时,
时,
kn=(p+![]() )n+(
)n+(![]() )n=(p+
)n=(p+![]() )n+(p-
)n+(p-![]() )n.
)n.
同理,当 x0=p-![]() 时,kn=(p+
时,kn=(p+![]() )n+(p-
)n+(p-![]() )n.
)n.
①当n=2m(m![]() N*)时, kn=2
N*)时, kn=2![]() ,所以kn为偶数.
,所以kn为偶数.
②当n=2m+1(m![]() N)时,kn=2
N)时,kn=2![]() ,所以kn为偶数.
,所以kn为偶数.
综上, kn为偶数.

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中 ,
,![]() .
.
【题目】“业务技能测试”是量化考核员工绩效等级的一项重要参考依据.某公司为量化考核员工绩效等级设计了A,B两套测试方案,现各抽取![]() 名员工参加A,B两套测试方案的预测试,统计成绩(满分
名员工参加A,B两套测试方案的预测试,统计成绩(满分![]() 分),得到如下频率分布表.
分),得到如下频率分布表.
成绩频率 |
|
|
|
|
|
|
|
方案A |
|
|
|
|
|
|
|
方案B |
|
|
|
|
|
|
|
(1)从预测试成绩在![]() 的员工中随机抽取
的员工中随机抽取![]() 人,记参加方案A的人数为
人,记参加方案A的人数为![]() ,求
,求![]() 的最有可能的取值;
的最有可能的取值;
(2)由于方案A的预测试成绩更接近正态分布,该公司选择方案A进行业务技能测试.测试后,公司统计了若干部门测试的平均成绩![]() 与绩效等级优秀率
与绩效等级优秀率![]() ,如下表所示:
,如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据数据绘制散点图,初步判断,选用![]() 作为回归方程.令
作为回归方程.令![]() ,经计算得
,经计算得![]() ,
,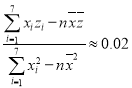 ,
,![]() .
.
(ⅰ)若某部门测试的平均成绩为![]() ,则其绩效等级优秀率的预报值为多少?
,则其绩效等级优秀率的预报值为多少?
(ⅱ)根据统计分析,大致认为各部门测试平均成绩![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于![]() 的概率为多少?
的概率为多少?
参考公式与数据:(1)![]() ,
,![]() ,
,![]() .
.
(2)线性回归方程![]() 中,
中,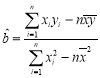 ,
,![]() .
.
(3)若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() .
.