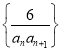题目内容
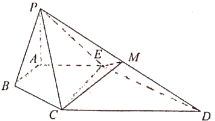
【题目】如图所示的几何体![]() 中,
中,![]() 和
和![]() 均为以
均为以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)设![]() 为线段
为线段![]() 上的动点,使得平面
上的动点,使得平面![]() 平面
平面![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题意,得出![]() ,
,![]() ,根据线面垂直的判定定理得出
,根据线面垂直的判定定理得出![]() 平面
平面![]() ,则
,则![]() ,建立以
,建立以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴的空间直角坐标系,利用向量法能证明
轴的空间直角坐标系,利用向量法能证明![]() ;
;
(2)求出平面![]() 的法向量和平面
的法向量和平面![]() 的一个法向量,利用向量法能求出二面角
的一个法向量,利用向量法能求出二面角![]() 的大小;
的大小;
(3)设![]() ,
,![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,
,![]() ,令
,令![]() ,则
,则![]() ,解得
,解得![]() 为
为![]() 的中点,利用向量法能求出线段
的中点,利用向量法能求出线段![]() 的长.
的长.
解:依题意得,![]() 和
和![]() 均为以
均为以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,
则![]() ,
,![]() ,
,
所以![]() 面
面![]() ,
,
又![]() ,可以建立以
,可以建立以![]() 为原点,
为原点,
分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
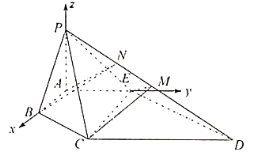
轴,![]() 轴正方向的空间直角坐标系(如图),
轴正方向的空间直角坐标系(如图),
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(1)证明:由题意,![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() .
.
(2)解:![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则
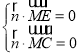 ,即
,即![]() ,
,
不妨令![]() ,可得
,可得![]() ,
,
平面![]() 的一个法向量
的一个法向量![]() ,
,
因此有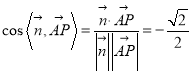 ,
,
由图可得二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的大小为
的大小为![]() .
.
(3)解:(方法一)设![]() ,
,![]() ,
,
所以![]() ,因此
,因此![]() ,
,
令![]() ,即
,即![]() ,
,
解得![]() ,即
,即![]() 为
为![]() 的中点,
的中点,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以当![]() 为
为![]() 的中点时,平面
的中点时,平面![]() 平面
平面![]() ,
,
此时即![]() ,
,
![]() ,
,
所以线段![]() 的长为
的长为![]() .
.
(方法二)设![]() ,
,![]() ,
,
所以![]() ,因此
,因此![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则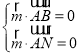 ,即
,即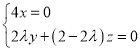 ,
,
不妨令![]() ,可得
,可得![]() ,
,
因为平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
解得:![]() ,
,
此时即![]() ,
,![]() ,
,
所以线段![]() 的长为
的长为![]() .
.

 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中 ,
,![]() .
.
【题目】“业务技能测试”是量化考核员工绩效等级的一项重要参考依据.某公司为量化考核员工绩效等级设计了A,B两套测试方案,现各抽取![]() 名员工参加A,B两套测试方案的预测试,统计成绩(满分
名员工参加A,B两套测试方案的预测试,统计成绩(满分![]() 分),得到如下频率分布表.
分),得到如下频率分布表.
成绩频率 |
|
|
|
|
|
|
|
方案A |
|
|
|
|
|
|
|
方案B |
|
|
|
|
|
|
|
(1)从预测试成绩在![]() 的员工中随机抽取
的员工中随机抽取![]() 人,记参加方案A的人数为
人,记参加方案A的人数为![]() ,求
,求![]() 的最有可能的取值;
的最有可能的取值;
(2)由于方案A的预测试成绩更接近正态分布,该公司选择方案A进行业务技能测试.测试后,公司统计了若干部门测试的平均成绩![]() 与绩效等级优秀率
与绩效等级优秀率![]() ,如下表所示:
,如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据数据绘制散点图,初步判断,选用![]() 作为回归方程.令
作为回归方程.令![]() ,经计算得
,经计算得![]() ,
,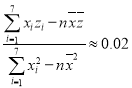 ,
,![]() .
.
(ⅰ)若某部门测试的平均成绩为![]() ,则其绩效等级优秀率的预报值为多少?
,则其绩效等级优秀率的预报值为多少?
(ⅱ)根据统计分析,大致认为各部门测试平均成绩![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于![]() 的概率为多少?
的概率为多少?
参考公式与数据:(1)![]() ,
,![]() ,
,![]() .
.
(2)线性回归方程![]() 中,
中,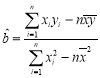 ,
,![]() .
.
(3)若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价![]() (单位:元/件)及相应月销量
(单位:元/件)及相应月销量![]() (单位:万件),对近5个月的月销售单价
(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下表数据:
的数据进行了统计,得到如下表数据:
月销售单价 | 9 |
| 10 |
| 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)该公司开展促销活动,当该产品月销售单价为7元/件时,其月销售量达到18万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() 万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
(Ⅲ)根据(Ⅰ)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中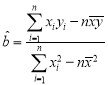 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.