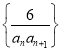��Ŀ����
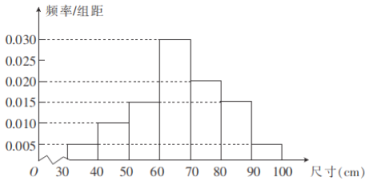
����Ŀ��Ϊ�˼����������ij��������������Ӳ�Ʒ�������ȡ100�������������ߴ磬�õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��������ߴ���������![]() ֮�ڣ�����Ϊ������ϸ�����Ϊ���ϸ�����
֮�ڣ�����Ϊ������ϸ�����Ϊ���ϸ�����![]() ��
��![]() �ֱ��ʾ������ƽ��ֵ�ͱ�������
�ֱ��ʾ������ƽ��ֵ�ͱ�������![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
��1����֪һ������ijߴ���![]() �����жϸ�����Ƿ�ϸ�
�����жϸ�����Ƿ�ϸ�
��2�����÷ֲ�����ķ����ӳߴ���![]() �������г�ȡ6��������ٴ���6������������ȡ2��������2�������ǡ��1���ߴ�С��
�������г�ȡ6��������ٴ���6������������ȡ2��������2�������ǡ��1���ߴ�С��![]() �ĸ��ʣ�
�ĸ��ʣ�
���𰸡���1����������ϸ�2��![]()
��������
��1������Ƶ�ʷֲ�ֱ��ͼ�������![]() �����䣬���ж�
�����䣬���ж�![]() �Ƿ����������ڣ����ɵô𰸣�
�Ƿ����������ڣ����ɵô𰸣�
��2������6��������Ϊ��![]() �����г�����6������������ȡ2���Ļ����¼������¼�
�����г�����6������������ȡ2���Ļ����¼������¼�![]() Ϊ����ѡ����2�������ǡ��1���ߴ�С��
Ϊ����ѡ����2�������ǡ��1���ߴ�С��![]() ���������¼�
���������¼�![]() �����Ļ����¼������ùŵ���ͼ�����ʣ����ɵô𰸣�
�����Ļ����¼������ùŵ���ͼ�����ʣ����ɵô𰸣�
��1���Ǹ����Ƶ��Ϊ![]() ���������
���������
![]() ��
��
![]()
��![]()
![]()
��![]()
��![]() ���ʸ�������ϸ�
���ʸ�������ϸ�
��2����ǰ�����ȡ����������ֱ�Ϊ![]()
��![]() ����
����![]()
���ȡ����6������гߴ�С��![]() ����3����
����3����
����6����������![]() ������
������![]() Ϊ�ߴ�С��
Ϊ�ߴ�С��![]() �ģ�
�ģ�
���¼�![]() Ϊ����ѡ����2�������ǡ��1���ߴ�С��
Ϊ����ѡ����2�������ǡ��1���ߴ�С��![]() ��
��
�����6������������ȡ2���Ļ����¼��У�
![]()
![]() ��15����
��15����
���¼�![]() �����Ļ����¼��У�
�����Ļ����¼��У�
![]() ��9��
��9��
��![]()
����2�������ǡ��1���ߴ�С��![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ��
��