题目内容
【题目】圆![]() ,直线
,直线![]() .
.
(1)证明:不论![]() 取什么数,直线
取什么数,直线![]() 与圆
与圆![]() 恒交于两点;
恒交于两点;
(2)求直线![]() 被圆
被圆![]() 截得的线段的最短长度,并求此时
截得的线段的最短长度,并求此时![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先由直线![]() 的方程得到定点坐标
的方程得到定点坐标![]() ,再判断出
,再判断出![]() 在圆内,即可得出结论;
在圆内,即可得出结论;
(2)由(1)可得,过点![]() 的所有弦中,弦心距
的所有弦中,弦心距![]() ,因此当
,因此当![]() 取最大值时,弦长最短,求出弦长,再由
取最大值时,弦长最短,求出弦长,再由![]() ,即可求出结果.
,即可求出结果.
(1)因为直线![]() 的方程可化为
的方程可化为![]() ,
,
所以![]() 过直线
过直线![]() 与
与![]() 的交点
的交点![]() .
.
又因为点![]() 到圆心
到圆心![]() 的距离
的距离![]() ,
,
所以点![]() 在圆内,所以过点
在圆内,所以过点![]() 的直线
的直线![]() 与圆
与圆![]() 恒交于两点.
恒交于两点.
(2)由(1)可知:过点![]() 的所有弦中,弦心距
的所有弦中,弦心距![]() ,
,
因为弦心距、半弦长和半径![]() 构成直角三角形,
构成直角三角形,
所以当![]() 时,半弦长的平方的最小值为
时,半弦长的平方的最小值为![]() ,
,
所以弦长的最小值为![]() .
.
此时,![]() .
.
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以当![]() 时,得到最短弦长为
时,得到最短弦长为![]() .
.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
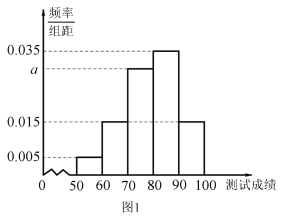
【题目】顺义区教委对本区高一,高二年级学生体质健康测试成绩进行抽样分析.学生测试成绩满分为100分,90分及以上为优秀,60分以下为不及格.先从两个年级各抽取100名学生的测试成绩.其中高一年级学生测试成绩统计结果如图1,高二年级学生测试成绩统计结果如表1.
分组 | 人数 |
|
|
|
|
|
|
|
|
|
|
表1
(1)求图1中a的值;
(2)为了调查测试成绩不及格的同学的具体情况,决定从样本中不及格的学生中抽取3人,用X表示抽取的3人中高二年级的学生人数.求X的分布列及均值;
(3)若用以上抽样数据估计全区学生体质健康情况.用Y表示从全区高二年级全部学生中任取3人中成绩优秀的人数,求EY的值;
(4)用![]() ,
,![]() ,分别表示样本中高一,高二年级学生测试成绩的方差,比较其大小(只需写出结果).
,分别表示样本中高一,高二年级学生测试成绩的方差,比较其大小(只需写出结果).