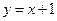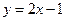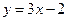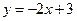题目内容
已知函数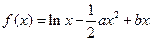 (
(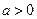 ),且
),且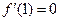 .
.
(Ⅰ)试用含有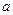 的式子表示
的式子表示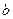 ,并求
,并求 的极值;
的极值;
(Ⅱ)对于函数 图象上的不同两点
图象上的不同两点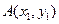 ,
,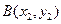 ,如果在函数图象上
,如果在函数图象上 存在点
存在点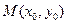 (其中
(其中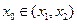 ),使得点
),使得点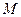 处的切线
处的切线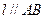 ,则称
,则称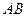 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当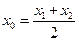 时,又称
时,又称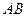 存在“中值伴随切线”. 试问:在函数
存在“中值伴随切线”. 试问:在函数 的图象上是否存在两点
的图象上是否存在两点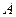 、
、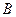 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出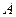 、
、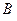 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
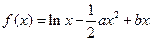 (
(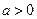 ),且
),且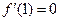 .
.(Ⅰ)试用含有
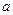 的式子表示
的式子表示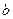 ,并求
,并求 的极值;
的极值;(Ⅱ)对于函数
 图象上的不同两点
图象上的不同两点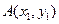 ,
,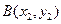 ,如果在函数图象上
,如果在函数图象上 存在点
存在点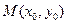 (其中
(其中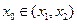 ),使得点
),使得点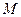 处的切线
处的切线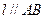 ,则称
,则称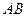 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当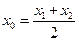 时,又称
时,又称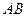 存在“中值伴随切线”. 试问:在函数
存在“中值伴随切线”. 试问:在函数 的图象上是否存在两点
的图象上是否存在两点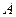 、
、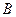 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出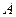 、
、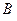 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.(Ⅰ)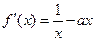
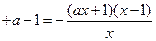 ,
,
当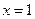 时,
时, 的极大值为
的极大值为
(Ⅱ)在函数 上不存在两点
上不存在两点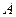 、
、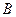 使得它存在“中值伴随切线”.理由略
使得它存在“中值伴随切线”.理由略
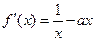
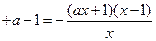 ,
,当
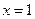 时,
时, 的极大值为
的极大值为
(Ⅱ)在函数
 上不存在两点
上不存在两点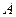 、
、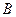 使得它存在“中值伴随切线”.理由略
使得它存在“中值伴随切线”.理由略(Ⅰ) 的定义域为
的定义域为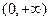 ,
,
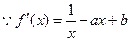 ,
,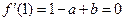 ,
,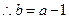 . ……………2分
. ……………2分
代入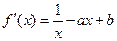 ,得
,得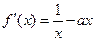
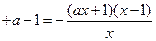 .
.
当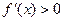 时,
时,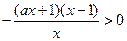 ,由
,由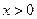 ,得
,得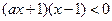 ,
,
又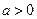 ,
,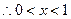 ,即
,即 在
在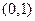 上单调递增;
上单调递增;
当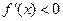 时,
时,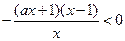 ,由
,由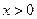 ,得
,得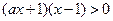 ,……………4分
,……………4分
又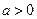 ,
,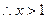 ,即
,即 在
在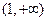 上单调递减.
上单调递减.
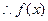 在
在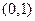 上单调递增,在
上单调递增,在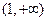 上单调递减.
上单调递减.
所以,当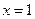 时,
时, 的极大值为
的极大值为 ………………6分
………………6分
(Ⅱ)在函数 的图象上不存在两点
的图象上不存在两点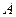 、
、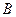 使得它存在“中值伴随切线”.
使得它存在“中值伴随切线”.
假设存在两点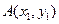 ,
,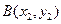 ,不妨设
,不妨设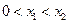 ,则
,则
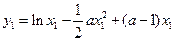 ,
,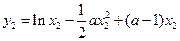 ,
,
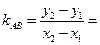
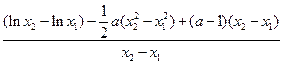
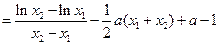 ,
,
在函数图象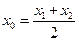 处的切线斜率
处的切线斜率
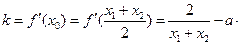
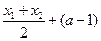 ,
,
由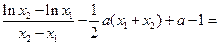
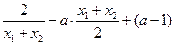
化简得: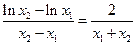 ,
,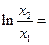
 .
.
令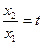 ,则
,则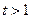 ,上式化为:
,上式化为: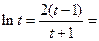
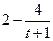 ,即
,即 ,
,
若令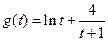 ,
,
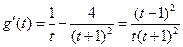 ,
,
由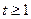 ,
,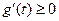 ,
,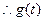 在
在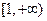 在上单调递增,
在上单调递增,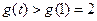 .
.
这表明在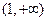 内不存在
内不存在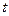 ,使得
,使得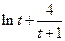 =2.
=2.
综上所述,在函数 上不存在两点
上不存在两点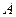 、
、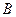 使得它存在“中值伴随切线”.…………13分
使得它存在“中值伴随切线”.…………13分
 的定义域为
的定义域为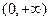 ,
,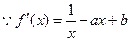 ,
,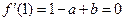 ,
,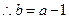 . ……………2分
. ……………2分代入
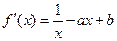 ,得
,得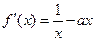
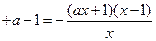 .
.当
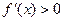 时,
时,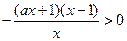 ,由
,由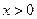 ,得
,得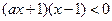 ,
,又
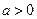 ,
,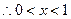 ,即
,即 在
在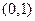 上单调递增;
上单调递增;当
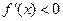 时,
时,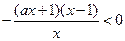 ,由
,由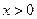 ,得
,得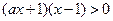 ,……………4分
,……………4分又
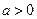 ,
,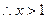 ,即
,即 在
在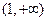 上单调递减.
上单调递减.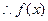 在
在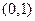 上单调递增,在
上单调递增,在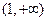 上单调递减.
上单调递减. 所以,当
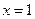 时,
时, 的极大值为
的极大值为 ………………6分
………………6分(Ⅱ)在函数
 的图象上不存在两点
的图象上不存在两点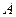 、
、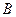 使得它存在“中值伴随切线”.
使得它存在“中值伴随切线”. 假设存在两点
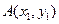 ,
,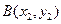 ,不妨设
,不妨设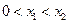 ,则
,则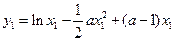 ,
,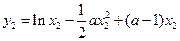 ,
,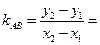
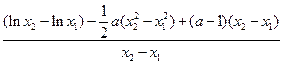
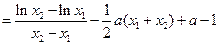 ,
,在函数图象
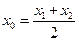 处的切线斜率
处的切线斜率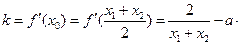
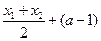 ,
,由
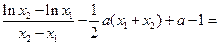
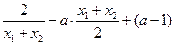
化简得:
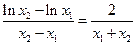 ,
,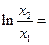
 .
.令
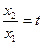 ,则
,则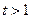 ,上式化为:
,上式化为: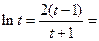
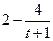 ,即
,即 ,
,若令
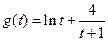 ,
,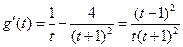 ,
, 由
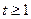 ,
,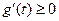 ,
,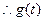 在
在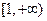 在上单调递增,
在上单调递增,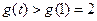 .
.这表明在
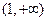 内不存在
内不存在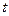 ,使得
,使得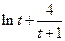 =2.
=2.综上所述,在函数
 上不存在两点
上不存在两点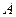 、
、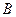 使得它存在“中值伴随切线”.…………13分
使得它存在“中值伴随切线”.…………13分
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
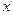 万套世博会吉祥物海宝所需成本费用为
万套世博会吉祥物海宝所需成本费用为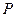 元,且
元,且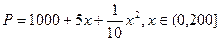 ,而每套售出价格为
,而每套售出价格为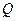 元,其中
元,其中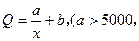
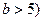 ,问:
,问: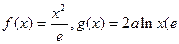 为自然对数的底数,
为自然对数的底数,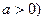
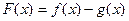 的单调区间,若
的单调区间,若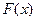 有最值,请求出最值;
有最值,请求出最值;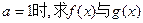 图象的一个公共点坐标,并求它们在该公共点处的切线方程。
图象的一个公共点坐标,并求它们在该公共点处的切线方程。
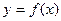 的图象在点P处的切线方程是
的图象在点P处的切线方程是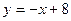 ,则
,则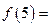 ,
,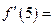
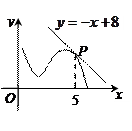
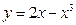 在
在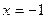 处的切线方程为 。
处的切线方程为 。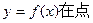
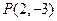 的切线方程为
的切线方程为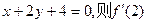 等于 ( )
等于 ( )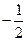
 3
3 知直线
知直线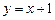 与曲线
与曲线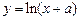 相切,则a的值为 ( )
相切,则a的值为 ( ) 
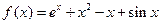 ,则曲线
,则曲线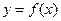 在点
在点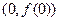 处的切线方程是
处的切线方程是