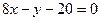题目内容
(本小题满分13分)
已知函数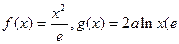 为自然对数的底数,
为自然对数的底数,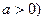
(1)求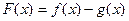 的单调区间,若
的单调区间,若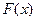 有最值,请求出最值;
有最值,请求出最值;
(2)当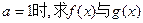 图象的一个公共点坐标,并求它们在该公共点处的切线方程。
图象的一个公共点坐标,并求它们在该公共点处的切线方程。
已知函数
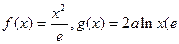 为自然对数的底数,
为自然对数的底数,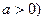
(1)求
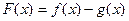 的单调区间,若
的单调区间,若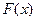 有最值,请求出最值;
有最值,请求出最值;(2)当
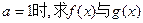 图象的一个公共点坐标,并求它们在该公共点处的切线方程。
图象的一个公共点坐标,并求它们在该公共点处的切线方程。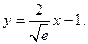
解:(1)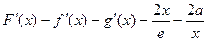
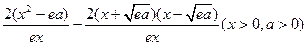 ………………3分
………………3分
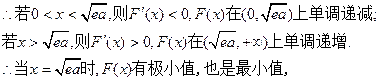
即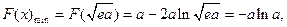 ………………7分
………………7分
所以当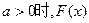 的单调递减区间为
的单调递减区间为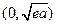 ,
,
单调递增区间为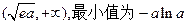 无最大值,………………8分
无最大值,………………8分
(2)当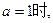 由(1)可知
由(1)可知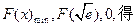
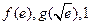 ,
,
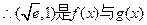 图象的一个公共点。 ………………11分
图象的一个公共点。 ………………11分
又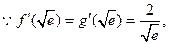
 处有共同的切线,
处有共同的切线,
其方程为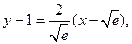
即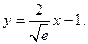 ………………13分
………………13分
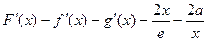
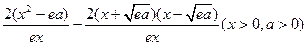 ………………3分
………………3分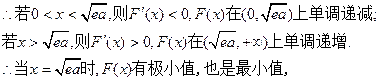
即
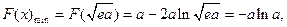 ………………7分
………………7分所以当
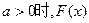 的单调递减区间为
的单调递减区间为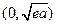 ,
,单调递增区间为
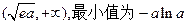 无最大值,………………8分
无最大值,………………8分(2)当
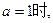 由(1)可知
由(1)可知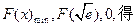
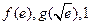 ,
,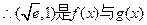 图象的一个公共点。 ………………11分
图象的一个公共点。 ………………11分又
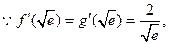
 处有共同的切线,
处有共同的切线,其方程为
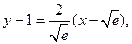
即
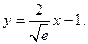 ………………13分
………………13分
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
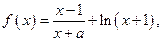 其中实数
其中实数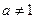 。
。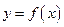 在点
在点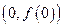 处的切线方程;
处的切线方程;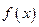 的单调性。
的单调性。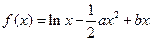 (
(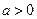 ),且
),且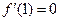 .
.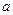 的式子表示
的式子表示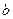 ,并求
,并求 的极值;
的极值;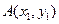 ,
,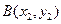 ,如果在函数图象上
,如果在函数图象上 存在点
存在点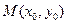 (其中
(其中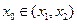 ),使得点
),使得点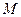 处的切线
处的切线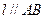 ,则称
,则称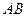 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当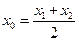 时,又称
时,又称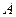 、
、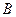 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出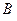 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.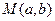 是曲线
是曲线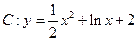 上的任意一点,直线
上的任意一点,直线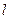 是曲线
是曲线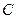 在点
在点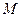 处的切线,那么直线
处的切线,那么直线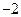
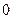
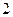
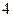
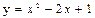 在点(0,1)处的切线方程为
在点(0,1)处的切线方程为 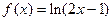 上的点到直线
上的点到直线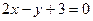 的最短距离是 ( )
的最短距离是 ( )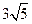
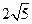
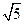
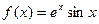 ,则此函数图象在点(4,f(4))处的切线的倾斜角为( )
,则此函数图象在点(4,f(4))处的切线的倾斜角为( )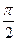
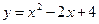 在点(1、3)外的切线的倾斜角为( )
在点(1、3)外的切线的倾斜角为( )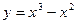 ,在
,在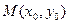
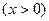 处切线斜率为8,则此切线方程是 ( )
处切线斜率为8,则此切线方程是 ( )