题目内容
设数列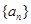 ,
,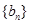 ,
,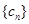 ,已知
,已知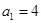 ,
,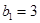 ,
,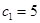 ,
,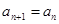 ,
,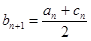 ,
,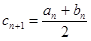 (
(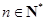 ).
).
(1)求数列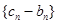 的通项公式;
的通项公式;
(2)求证:对任意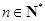 ,
, 为定值;
为定值;
(3)设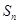 为数列
为数列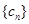 的前
的前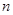 项和,若对任意
项和,若对任意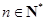 ,都有
,都有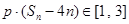 ,求实数
,求实数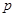 的取值范围.
的取值范围.
(1)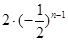 ;(2)证明见解析;(3)
;(2)证明见解析;(3)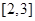 .
.
解析试题分析:(1)根据已知条件与待求式,作差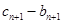 ,可得
,可得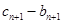
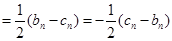 ,而
,而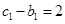 ,故数列
,故数列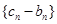 是等比数列,通项公式可求;(2)考虑要证的表达式求和
是等比数列,通项公式可求;(2)考虑要证的表达式求和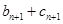
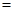
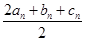 ,表面上看不出什么,但由
,表面上看不出什么,但由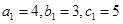 ,可得
,可得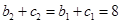 ,由由
,由由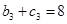 ,可以想象
,可以想象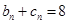 ,是常数,因此可用数学归纳法证明;(3)由(1)(2)可解得
,是常数,因此可用数学归纳法证明;(3)由(1)(2)可解得 ,那么其前
,那么其前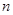 项和
项和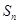 可用分组求和法求得,
可用分组求和法求得,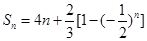 ,这样我们就可求出
,这样我们就可求出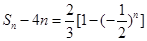 ,
,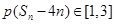 ,相当于
,相当于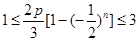 ,由于
,由于 ,从而
,从而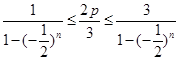 ,一直是我们只要求得
,一直是我们只要求得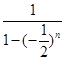 的最大值
的最大值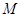 和
和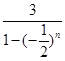 的最小值
的最小值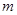 ,则就是
,则就是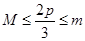 ,由此可求得
,由此可求得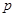 的范围.
的范围.
试题解析:(1)因为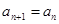 ,
,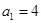 ,所以
,所以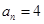 (
(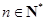 ), (1分)
), (1分)
所以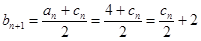 ,
,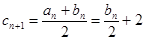 ,
,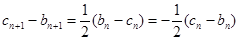 , (2分)
, (2分)
即数列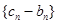 是首项为
是首项为 ,公比为
,公比为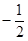 的等比数列, (3分)
的等比数列, (3分)
所以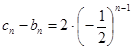 . (4分)
. (4分)
(2)解法一: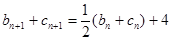 , (1分)
, (1分)
因为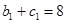 ,所以
,所以 ,
,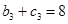 ,
,
猜测: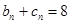 (
(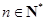 ). (2分)
). (2分)
用数学归纳法证明:
①当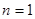 时,
时,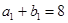 ,结论成立; (3分)
,结论成立; (3分)
②假设当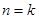 (
(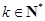 )时结论成立,即
)时结论成立,即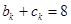 ,那么当
,那么当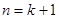 时,
时,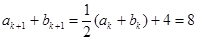 ,即
,即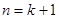 时结论也成立. (5分)
时结论也成立. (5分)
由①,②得,当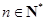 时,
时,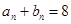 恒成立,即
恒成立,即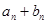 恒为定值.(6分)
恒为定值.(6分)
解法二: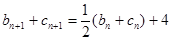 , (1分)
, (1分)
所以 ,(4分)
,(4分)
而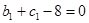 ,所以由上述递推关系可得,当
,所以由上述递推关系可得,当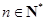 时,
时,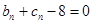 恒成立,即
恒成立,即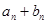 恒为定值.(6分)
恒为定值.(6分)
(3)由(1)、(2)知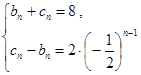 ,所以
,所以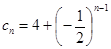 ,(1分)
,(1分)
所以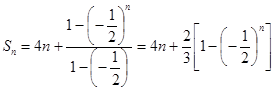 ,
,
所以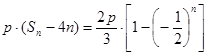 , (2分)
, (2分)
由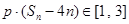 得
得 ,
,
因为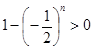 ,所以
,所以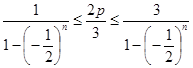

练习册系列答案
相关题目
 中,
中, ,
, ,
, ,
, 分别为△ABC的三个内角A,B,C的对边,且
分别为△ABC的三个内角A,B,C的对边,且 .
.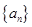 的公比
的公比 ;
; ,且
,且 ,求数列
,求数列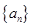 和
和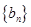 满足:
满足: ,其中
,其中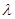 为实数,
为实数,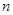 为正整数.
为正整数. 不成等比数列;
不成等比数列;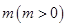 万吨.
万吨.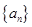 ,求相邻两年主要污染物排放总量的关系式;
,求相邻两年主要污染物排放总量的关系式;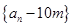 是等比数列;
是等比数列;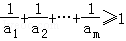 ?若存在,求m的最小值;若不存在,说明理由.
?若存在,求m的最小值;若不存在,说明理由.
 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有 改选A菜。用
改选A菜。用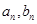 分别表示第
分别表示第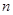 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数.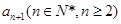 表示
表示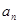 ,判断数列
,判断数列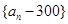 是否成等比数列并说明理由;
是否成等比数列并说明理由;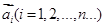 排成一列,称为向量列,记作
排成一列,称为向量列,记作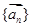 ,又设
,又设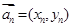 ,假设向量列
,假设向量列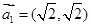 ,
,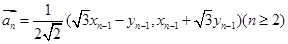 。
。 是等比数列;
是等比数列;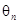 表示向量
表示向量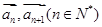 间的夹角,若
间的夹角,若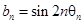 ,记
,记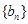 的前
的前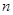 项和为
项和为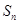 ,求
,求 ;
;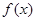 是
是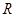 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的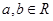 ,都有
,都有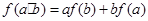 ,若
,若 ,
,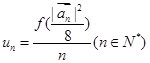 ,求数列
,求数列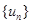 的前
的前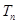 .
.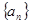 的前
的前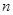 项和
项和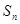 满足
满足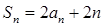
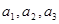 ;
;