题目内容
等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:bn=an+(-1)nlnan,求数列{bn}的前n项和Sn·
(1) =2·
=2·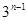 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(Ⅰ)此问首先要结合所给列表充分讨论符合要求的所有情况,根据符合的情况进一步分析公比进而求得数列{an}的通项公式;
(Ⅱ)首先要利用第(Ⅰ)问的结果对数列数列{bn}的通项进行化简,然后结合通项的特点,利用分组法进行数列{bn}的前n项和的求解 .
试题解析:解:(1)当 时,不合题意
时,不合题意
当 时,当且仅当
时,当且仅当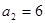 ,
,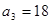 符合题意
符合题意
当 时,不合题意
时,不合题意
因此 ,
,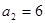 ,
,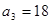 ,所以公比q=3
,所以公比q=3
故  =2·
=2·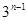
(2)∵ =2·
=2·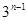 +
+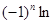 (2·
(2·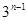 )=2·
)=2·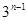 +
+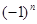 [ln2+(n-1)ln3]
[ln2+(n-1)ln3]
=2·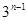 +
+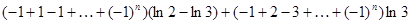
∴当n为偶数时, 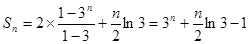
当n为奇数时,  =
=
考点:1.数列的求和;2.等比数列;3.数列递推式.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 是公比为
是公比为 的等比数列,推导
的等比数列,推导 项公式.
项公式. 满足条件:存在正整数
满足条件:存在正整数 ,使得
,使得 对一切
对一切 都成立,则称数列
都成立,则称数列 ,求
,求 的值;
的值; 为常数),且
为常数),且 级等比数列,求
级等比数列,求 所有可能值的集合,并求
所有可能值的集合,并求 项和
项和 ;
; 级等比数列,
级等比数列, 的各项均为正数,且
的各项均为正数,且
 求数列
求数列 的前n项和.
的前n项和. ,
, ,
,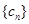 ,已知
,已知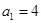 ,
,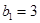 ,
,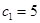 ,
,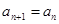 ,
,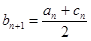 ,
,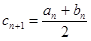 (
(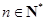 ).
).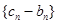 的通项公式;
的通项公式;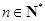 ,
, 为定值;
为定值;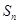 为数列
为数列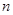 项和,若对任意
项和,若对任意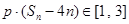 ,求实数
,求实数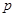 的取值范围.
的取值范围. ,定义
,定义 它的第
它的第 项为
项为
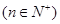 ,假设
,假设 是首项是
是首项是 公比为
公比为 的等比数列.
的等比数列. 的前
的前 ;
; ,
, ,
, .
. ;
; .
. 的通项公式为
的通项公式为 ,等比数列
,等比数列 满足
满足 .
. 项和
项和 ;
; ,求数列
,求数列 的前
的前 项和
项和 .
.