题目内容
我们把一系列向量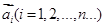 排成一列,称为向量列,记作
排成一列,称为向量列,记作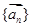 ,又设
,又设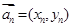 ,假设向量列
,假设向量列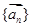 满足:
满足: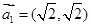 ,
,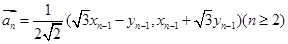 。
。
(1)证明数列 是等比数列;
是等比数列;
(2)设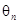 表示向量
表示向量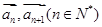 间的夹角,若
间的夹角,若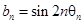 ,记
,记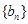 的前
的前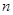 项和为
项和为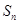 ,求
,求 ;
;
(3)设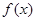 是
是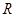 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的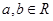 ,都有
,都有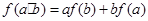 ,若
,若 ,
,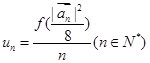 ,求数列
,求数列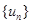 的前
的前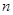 项和
项和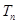 .
.
(1)证明过程见试题解析(2)当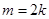 时,
时,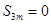 ;当
;当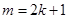 时,
时,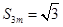 (3)
(3)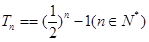
解析试题分析:(1)由向量的坐标运算可得 ,命题可证;(2)先求出
,命题可证;(2)先求出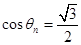 ,可得
,可得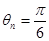 从而
从而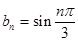 由通项公式可求出
由通项公式可求出 ;(3)先由特值法求出
;(3)先由特值法求出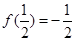 ,由所给条件可得
,由所给条件可得 ,从而求出
,从而求出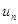 的通项公式,进一步求出前
的通项公式,进一步求出前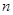 项和
项和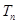 .
.
试题解析:解:(1)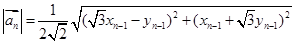
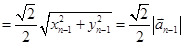 ,∴数列
,∴数列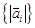 是等比数列
是等比数列
(2)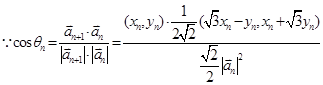
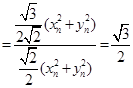
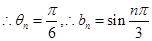 ,∴当
,∴当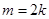 时,
时,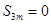 ;当
;当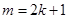 时,
时,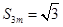 ;
;
(3)令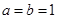 ,得
,得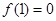 ,令
,令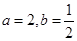 ,得
,得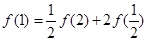 ,∴
,∴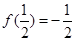
当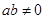 时,
时,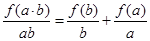 ,令
,令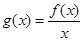 ,则
,则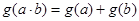 ,
,
故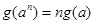 ,所以
,所以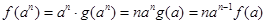 ,
,
所以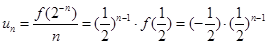 ,因此
,因此 。
。
考点:向量的数量积,构造法,等比数列的前n项和,逻辑推理能力.

练习册系列答案
相关题目
 满足
满足 ,
, .
. ,证明:
,证明: 是等比数列;
是等比数列;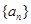 ,
,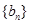 ,
,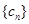 ,已知
,已知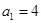 ,
,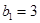 ,
,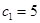 ,
,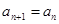 ,
,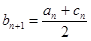 ,
,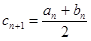 (
(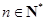 ).
).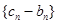 的通项公式;
的通项公式;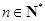 ,
, 为定值;
为定值;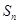 为数列
为数列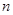 项和,若对任意
项和,若对任意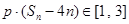 ,求实数
,求实数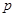 的取值范围.
的取值范围. 的通项公式为
的通项公式为 ,等比数列
,等比数列 满足
满足 .
. 项和
项和 ;
; ,求数列
,求数列 的前
的前 项和
项和 .
.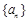 各项都是正数,
各项都是正数,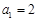 ,
,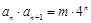 ,
, .
.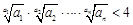 .
. ,an+1<an.
,an+1<an.