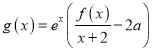题目内容
【题目】已知数列{an}是等差数列，且a1=2，a1+a2+a3=12．
（1）求数列{an}的通项公式；
（2）令bn=an3n（x∈R）．求数列{bn}前n项和的公式．
【答案】
（1）解：设数列{an}公差为d，则 a1+a2+a3=3a1+3d=12，
又a1=2，d=2．所以an=2n．
（2）解：由bn=an3n=2n3n，得
Sn=23+432+…（2n﹣2）3n﹣1+2n3n，①
3Sn=232+433+…+（2n﹣2）3n+2n3n+1．②
将①式减去②式，得
﹣2Sn=2（3+32+…+3n）﹣2n3n+1=﹣3（3n﹣1）﹣2n3n+1．
所以 
【解析】（1）利用等差数列的通项公式将已知等式用公差表示，列出方程求出公差，利用等差数列的通项公式求出通项．（2）由于数列的通项是一个等差数列与一个等比数列的乘积，利用错位相减法求前n项和．
【考点精析】本题主要考查了等差数列的通项公式（及其变式）和数列的前n项和的相关知识点，需要掌握通项公式：
或
；数列{an}的前n项和sn与通项an的关系
才能正确解答此题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
