题目内容
【题目】（本小题满分8分） 已知抛物线C：y=-x2+4x-3 ．
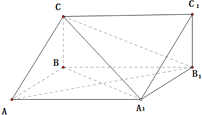
（1）求抛物线C在点A（0，－3）和点B（3，0）处的切线的交点坐标；
（2）求抛物线C与它在点A和点B处的切线所围成的图形的面积．
【答案】（1） （
）；（2）
．
【解析】试题分析：（1）首先求出抛物线的导数，然后分别求当
或，当
处的导数，再利用导数的几何意义知道导数即斜率，列出切线方程，最后解方程组，求交点坐标．（2）根据交点坐标
知，结合图像，根据定积分的面积的应用，知被积区间被分成
两部分，然后列出夹在两函数之间的面积计算表示．
试题解析：（1）
， 
，
所以过点A（0，－3）和点B（3，0）的切线方程分别是
，
两条切线的交点是（
），
（2）围成的区域如图所示：区域被直线
分成了两部分，分别计算再相加，得：
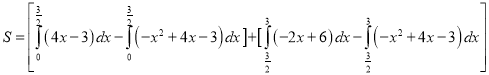
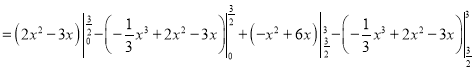
即所求区域的面积是
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为调查某地人群年龄与高血压的关系，用简单随机抽样方法从该地区年龄在20～60岁的人群中抽取200人测量血压，结果如下：
高血压 | 非高血压 | 总计 | |
年龄20到39岁 | 12 |
| 100 |
年龄40到60岁 |
| 52 | 100 |
总计 | 60 |
| 200 |
(1)计算表中的
、
、
值；是否有99%的把握认为高血压与年龄有关？并说明理由．
(2)现从这60名高血压患者中按年龄采用分层抽样的方法抽取5人，再从这5人中随机抽取2人，求恰好一名患者年龄在20到39岁的概率.
附参考公式及参考数据： 
=
P(k2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
