Question

【题目】已知二次函数f（x）=x2﹣16x+q+3：
（1）若函数在区间[﹣1，1]上存在零点，求实数q的取值范围；
（2）问：是否存在常数t（t≥0），当x∈[t，10]时，f（x）的值域为区间D，且D的长度为12﹣t．

Answer 1

【答案】
（1）解：∵二次函数f（x）=x2﹣16x+q+3的对称轴是x=8

∴函数f（x）在区间[﹣1，1]上单调递减

∴要使函数f（x）在区间[﹣1，1]上存在零点，须满足f（﹣1）f（1）≤0．

即（1+16+q+3）（1﹣16+q+3）≤0

解得﹣20≤q≤12．

所以使函数f（x）在区间[﹣1，1]上存在零点的实数q的取值范围是[﹣20，12]

（2）解：当 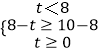时，即0≤t≤6时，f（x）的值域为：[f（8），f（t）]，

即[q﹣61，t2﹣16t+q+3]．

∴t2﹣16t+q+3﹣（q﹣61）=t2﹣16t+64=12﹣t．

∴t2﹣15t+52=0，∴ ．

经检验 不合题意，舍去．

当 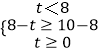时，即6≤t＜8时，f（x）的值域为：[f（8），f（10）]，

即[q﹣61，q﹣57]．

∴q﹣57﹣（q﹣61）=4=12﹣t．

∴t=8

经检验t=8不合题意，舍去．

当t≥8时，f（x）的值域为：[f（t），f（10）]，

即[t2﹣16t+q+3，q﹣57]

∴q﹣57﹣（t2﹣16t+q+3）=﹣t2+16t﹣60=12﹣t

∴t2﹣17t+72=0，∴t=8或t=9．

经检验t=8或t=9满足题意，

所以存在常数t（t≥0），当x∈[t，10]时，f（x）的值域为区间D，且D的长度为12﹣t

【解析】（1）求出二次函数的对称轴，得到函数f（x）在[﹣1，1]上为单调函数，要使函数在区间[﹣1，1]上存在零点，则f（﹣1）f（1）≤0，由此可解q的取值范围；（2）分t＜8，最大值是f（t）；t＜8，最大值是f（10）；8≤t＜10三种情况进行讨论，对于每一种情况，由区间长度是12﹣t求出t的值，验证范围后即可得到答案．
【考点精析】通过灵活运用二次函数的性质和函数的零点，掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减；函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点即可以解答此题．