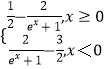题目内容
【题目】已知函数f（x）=（log2x）2﹣4log2x+1．
（1）求f（8）的值；
（2）当2≤x≤16时，求f（x）的最大值和最小值．
【答案】
（1）解：∵函数 
，
∴f（8）= 
=9﹣4×3+1=﹣2
（2）解：当2≤x≤16时，1≤log2x≤4． 令 t=log2x，则1≤t≤4，f（x）=t2﹣4t+1=（t﹣2）2﹣3，
故当t=2时，f（x）取得最小值为﹣3，当t=4时，f（x）取得最大值为 1
【解析】（1）根据函数的解析式可得f（8）= ，再利用对数的运算性质，求出结果．（2）当2≤x≤16时，令 t=log2x，则1≤t≤4，f（x）=t2﹣4t+1=（t﹣2）2﹣3，根据二次函数的性质求出f（x）的最大值和最小值．
【题目】某险种的基本保费为
（单位：元），继续购买该险种的投保人称为续保人，
续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况，得到如下统计表：
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 120 | 100 | 60 | 60 | 40 | 20 |
（Ⅰ）记A为事件：“一续保人本年度的保费不高于基本保费”.求
的估计值；
（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的190％”.
求
的估计值；
（III）求续保人本年度的平均保费估计值.
【题目】“累积净化量
”是空气净化器质量的一个重要衡量指标，它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量，以克表示，根据
《空气净化器》国家标准，对空气净化器的累计净化量有如下等级划分：
累积净化量（克） |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器（共5000台）的质量，随机抽取
台机器作为样本进行估计，已知这台机器的累积净化量都分布在区间
中，按照
、
、
、
、
均匀分组，其中累积净化量在的所有数据有：4.5,4.6,5.2,5.3,5.7和5.9，并绘制了频率分布直方图，如图所示：
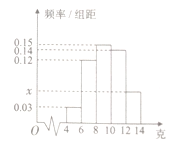
（1）求的值及频率分布直方图中
的值；
（2）以样本估计总体，试估计这批空气净化器（共5000台）中等级为
的空气净化器有多少台？
（3）从累积净化量在的样本中随机抽取2台，求恰好有1台等级为的概率.
