如图.某几何体的正视图.侧视图.俯视图均为面积为2的等腰直角三角形.则该多面体面的个数为4.体积为$\frac{4}{3}$．题目和参考答案——青夏教育精英家教网——

题目内容

16．

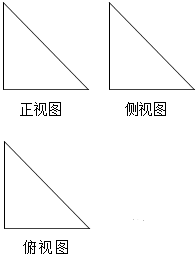如图，某几何体的正视图、侧视图、俯视图均为面积为2的等腰直角三角形，则该多面体面的个数为4，体积为$\frac{4}{3}$．

分析判断该几何体的正视图、侧视图、俯视图均为面积为2的等腰直角三角形，利用面的特点，得出线段，运用公式求解几何体的体积．

解答解：∵该几何体的正视图、侧视图、俯视图均为面积为2的等腰直角三角形，
∴该几何体是一个三棱锥，OA=OB=OC=2，OA，OB，OC两两垂直，
即该多面体面的个数为4，体积为；$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{3}$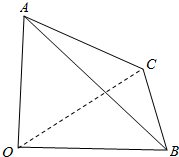

故答案为：4，$\frac{4}{3}$

点评本题考查了空间几何体的三视图的运用，恢复几何体的直观图，判断棱长，直线平面的位置关系，属于中档题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

17．若函数y=lg（x²+ax+a+$\frac{5}{4}$）的定义域为R，则a的取值范围为（-1，5）．

7．直三棱锥ABC-A₁B₁C₁中，∠BCA=90°，M，N分别是A₁B₁，A₁C₁的中点，BC=CA=CC₁，则BM与AN所成角的余弦值为（　　）

$\frac{\sqrt{2}}{2}$

$\frac{\sqrt{30}}{10}$

4．某市一所高中随机抽取部分高一学生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．

（Ⅰ）求直方图中x的值；
（Ⅱ）如果上学路上所需时间不少于1小时的学生可申请在学校住宿，若招生1200名，请估计新生中有多少名学生可以申请住宿；
（Ⅲ）从学校的高一学生中任选4名学生，这4名学生中上学路上所需时间少于20分钟的人数记为X，求X的分布列和数学期望．（以直方图中的频率作为概率）

11．已知集合U={1，2，3，4，5}，A={1，2，3}，B={2，4}，则A∩（∁_UB）=（　　）

{1，2，3，5}

1．已知a∈R，函数f（x）=x²-a|x-1|．
（Ⅰ）当a=1时，求函数f（x）的最小值；
（Ⅱ）讨论y=f（x）的图象与y=|x-a|的图象的公共点个数．

8．执行如图所示的程序框图，如果输入的t∈[-2，2]，则输出的S的取值范围是[-3，6]

5．在平面直角坐标系xOy中，直线l的方程为$\left\{\begin{array}{l}x=2+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.（t$为参数），以原点O为极点，Ox轴为极轴，取相同的单位长度，建立极坐标系，曲线犆的方程为ρ=4cosθ．
（1）求直线l的普通方程与曲线C的直角坐标方程；
（2）设点A（2+2cosα，2sinα），$B（5\sqrt{2}+\frac{{\sqrt{2}}}{2}t，2-\frac{{\sqrt{2}}}{2}t）$，求|AB|的最小值．（其中α?t为参数）

6．已知全集为R，集合A=$\left\{{\left.x\right|{{（{\frac{1}{2}}）}^x}≤1}\right\}$，B={x||x-3|≤1}，则A∩C_RB=（　　）

{x|0≤x＜2或x＞4}

{x|0＜x≤2或x≥4}