题目内容

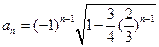 ,
,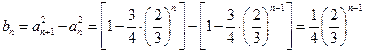
解:(Ⅰ)由题意可知,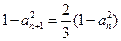
令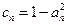 ,则
,则 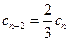
又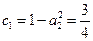 ,则数列
,则数列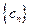 是首项为
是首项为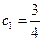 ,公比为
,公比为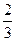 的等比数列,即
的等比数列,即
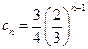 ,故
,故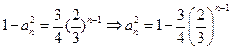 ,
,
又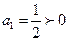 ,
,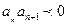
故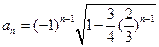
(Ⅲ)解法一:由(Ⅱ)知:当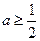 时,有
时,有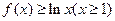 。
。
令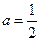 ,有
,有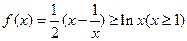
当 时,
时, 。
。
令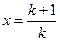 ,有
,有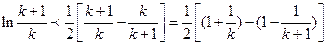
即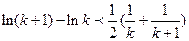 ,
,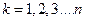
将上述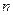 个不等式一次相加得
个不等式一次相加得

整理得
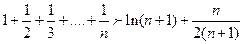
解法二:用数学归纳法证明
(1) 当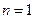 时,左边
时,左边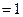 ,右边
,右边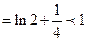 ,不等式成立
,不等式成立
(2) 假设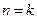 时, 不等式成立, 就是
时, 不等式成立, 就是
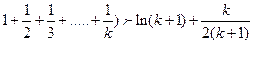
那么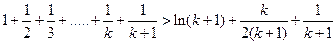
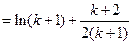
由(Ⅱ)知:当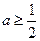 时,有
时,有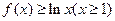
令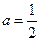 ,有
,有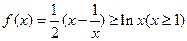
令 ,得:
,得:
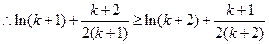
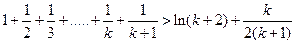
就是说,当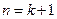 时,不等式也成立。
时,不等式也成立。
根据(1)和(2),可知不等式对任何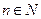 都成立。
都成立。
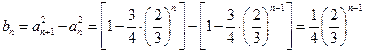
(Ⅱ)用反证法证明
假设数列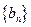 存在三项
存在三项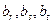
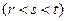 按某种顺序成等差数列,由于数列
按某种顺序成等差数列,由于数列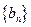 是首项为
是首项为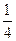 ,公比为
,公比为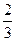 的等比数列,于是有
的等比数列,于是有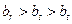 ,则只有可能有
,则只有可能有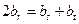 成立
成立
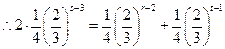
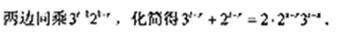
由于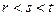 ,所以上式左边为奇数,右边为偶数,故上上式不可能成立,导致矛盾。故数列
,所以上式左边为奇数,右边为偶数,故上上式不可能成立,导致矛盾。故数列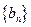 中任意三项不可能成等差数列。
中任意三项不可能成等差数列。
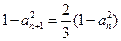
令
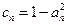 ,则
,则 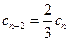
又
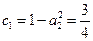 ,则数列
,则数列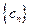 是首项为
是首项为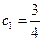 ,公比为
,公比为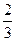 的等比数列,即
的等比数列,即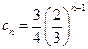 ,故
,故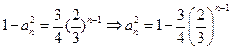 ,
,又
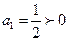 ,
,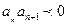
故
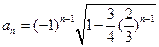
(Ⅲ)解法一:由(Ⅱ)知:当
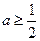 时,有
时,有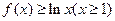 。
。令
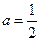 ,有
,有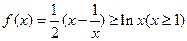
当
 时,
时, 。
。令
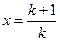 ,有
,有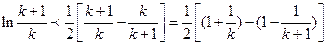
即
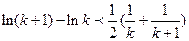 ,
,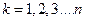
将上述
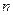 个不等式一次相加得
个不等式一次相加得
整理得
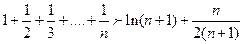
解法二:用数学归纳法证明
(1) 当
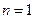 时,左边
时,左边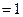 ,右边
,右边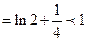 ,不等式成立
,不等式成立(2) 假设
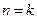 时, 不等式成立, 就是
时, 不等式成立, 就是 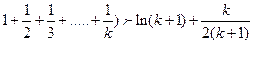
那么
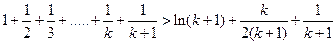
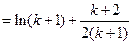
由(Ⅱ)知:当
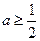 时,有
时,有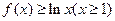
令
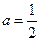 ,有
,有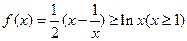
令
 ,得:
,得:
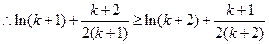
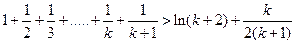
就是说,当
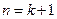 时,不等式也成立。
时,不等式也成立。根据(1)和(2),可知不等式对任何
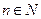 都成立。
都成立。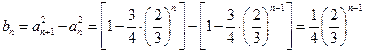
(Ⅱ)用反证法证明
假设数列
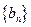 存在三项
存在三项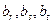
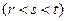 按某种顺序成等差数列,由于数列
按某种顺序成等差数列,由于数列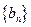 是首项为
是首项为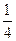 ,公比为
,公比为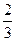 的等比数列,于是有
的等比数列,于是有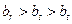 ,则只有可能有
,则只有可能有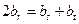 成立
成立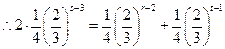
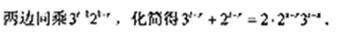
由于
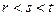 ,所以上式左边为奇数,右边为偶数,故上上式不可能成立,导致矛盾。故数列
,所以上式左边为奇数,右边为偶数,故上上式不可能成立,导致矛盾。故数列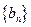 中任意三项不可能成等差数列。
中任意三项不可能成等差数列。
练习册系列答案
相关题目
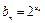 ,求数列{bn}的前n和Sn.
,求数列{bn}的前n和Sn.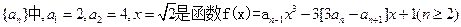 的一个极值点。
的一个极值点。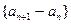 是等比数列;
是等比数列;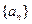 的通项公式;
的通项公式;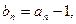
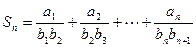 ,求证:
,求证: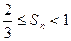
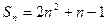 ,数列{bn}满足b1+3b2+…+(2n-1)b
,数列{bn}满足b1+3b2+…+(2n-1)b n=(2n―3)·2n+1,
n=(2n―3)·2n+1, ,若数列
,若数列 满足
满足 ,数列
,数列 ,则
,则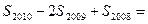 ( )
( )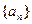 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,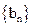 是首项为1,公比为3的等比数列,
是首项为1,公比为3的等比数列,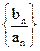 的前n项和
的前n项和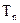 。
。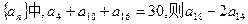 的值为 ( )
的值为 ( )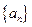 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,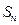 为
为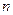 项和.
项和.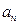 及
及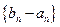 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列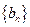 的通项公式及其前
的通项公式及其前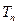 .
.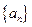 中,
中,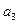 +
+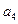 +
+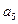 =12,那么
=12,那么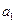 +
+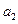 +•••…+
+•••…+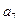 =
=